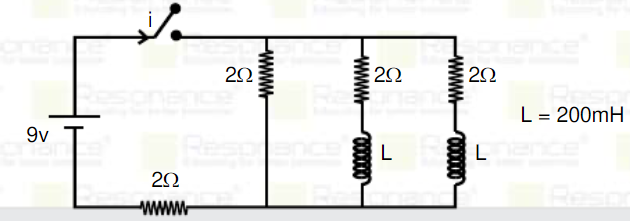
Figure shows an LCR circuit. When the switch is closed, the currents through resistor R, inductor L, and capacitor C are I1,I2, and I3, respectively. Determine the values of I1,I2, and I3.
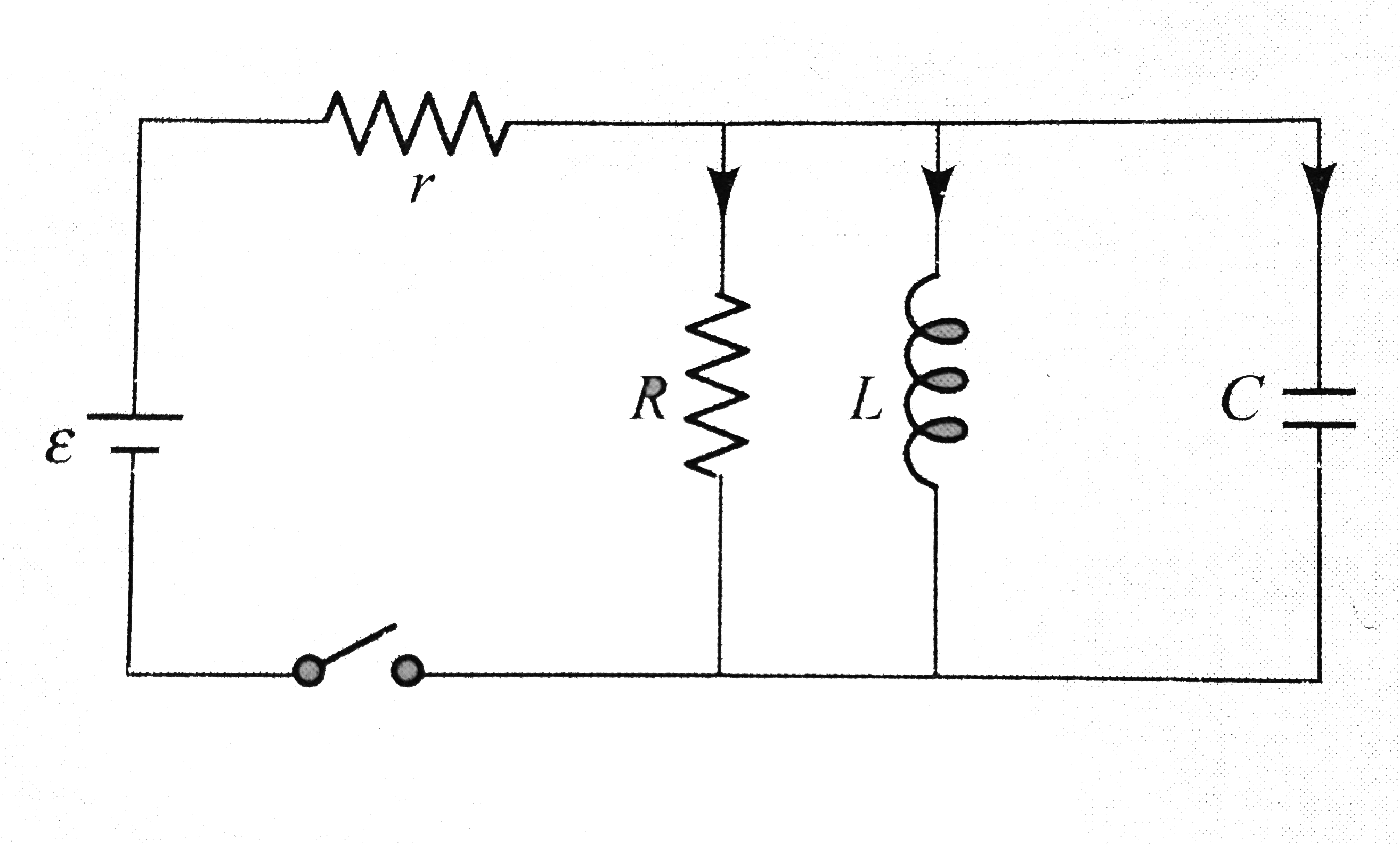
a. at t=0 b. at t=∞
At t=0, C will act as a simple wire, so R and L both will be short-circuited. So that there is no current in R and L.
I1=0,I2=0,I3=εr
At t=∞, will act as as a simple wire so, R and C will be short-circuited.
I1=0,I2=εr,I3=0
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (single Correct )
65 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Solved Examples
3 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
Knowledge Check
In the circuit shown, the switch is closed at t=0, the currents I1,I2 and I3 are
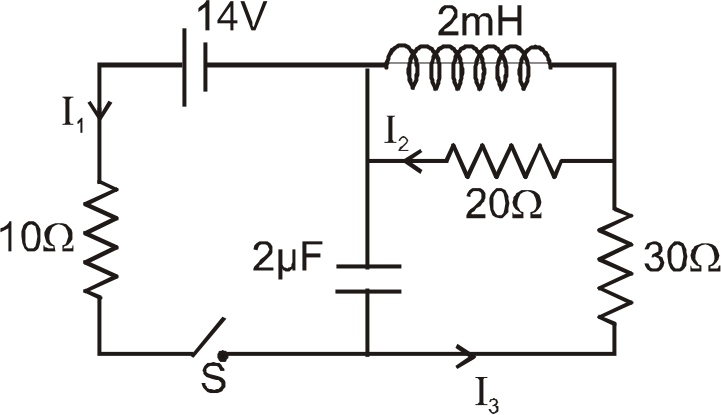 A1.4A,0,0B1.4 A,0.70 A,0.70 AC0,0,0D1.2A,0.6A,0.6A
A1.4A,0,0B1.4 A,0.70 A,0.70 AC0,0,0D1.2A,0.6A,0.6AIn the circuit shown, the value of currents I1,I2andI3 are
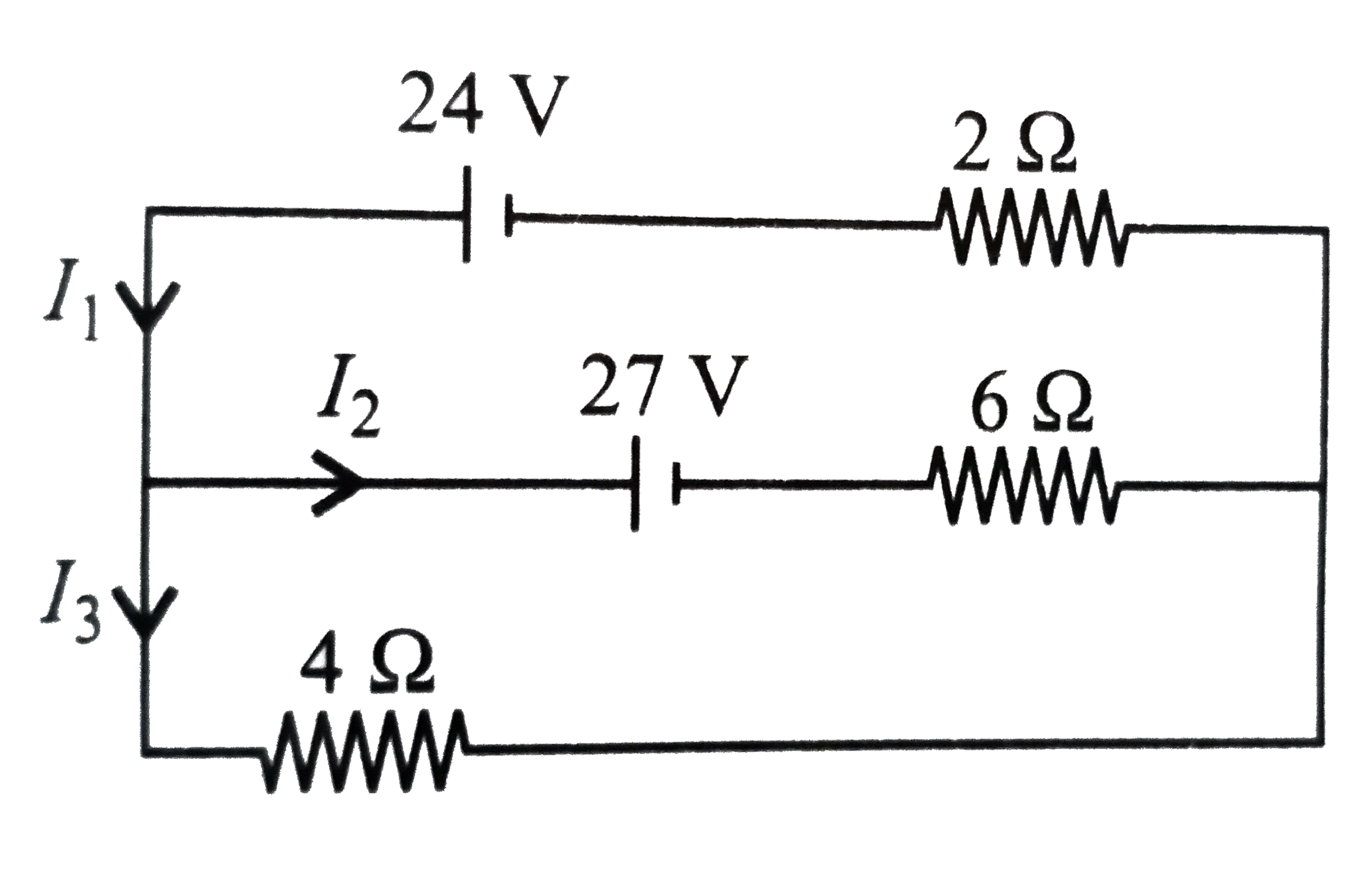 A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A
A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92AFind the current I1, I2, & I3, in the circuit.
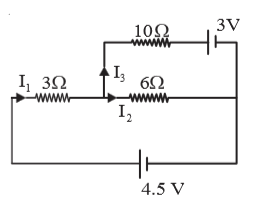 A12,12,1B1,1,2C12,12,3D12,12,0
A12,12,1B1,1,2C12,12,3D12,12,0

Determine the currents I1,I2andI3 from the network shown in figure.
View Solution
Find currents I1,I2 and I3 and the energy stored in the capacitors C1andC2 in the circuit shown in figure.
View SolutionThe figure shows three straight current carrying conductors having current I1,I2 and I3 respectively. Calculate line integral of magnetic induction field →B along the closed path ABCDEFA

View SolutionIn an L−R−C circuit the current is given by i=Icosωt. The voltage amplitudes for the resistor. Inductor and capacitor are VR,VL and VC respectively.
(a) The instantaneous power into the resistor is PR=VRIcos2ωt.
(b) The instantaneous into the inductor is PL=−VLIsinωtcosωt
(c ) The instantaneous power into the capacitor is Pc=VcIsinωtcosωt.
(d) pR+pL+Pc equals total power p supplied by the source at each instant of time.
View SolutionIn the figure shown, a conducting wire PQ of length l=1m, is moved in a uniform magnetic field B=4T with constant velocity v=2m/s towards right. Given R=2Ω,C=1FandL=4H.

Currents through resistor, capacitor and inductor at any time t are l1,I2andI3 respectively. Current through wire PQ is I.
At l=2s, the value of I3 is
View Solution