Figure shows the displacement-time graphs of two simple harmonic motions I and II. From the graph it follows that
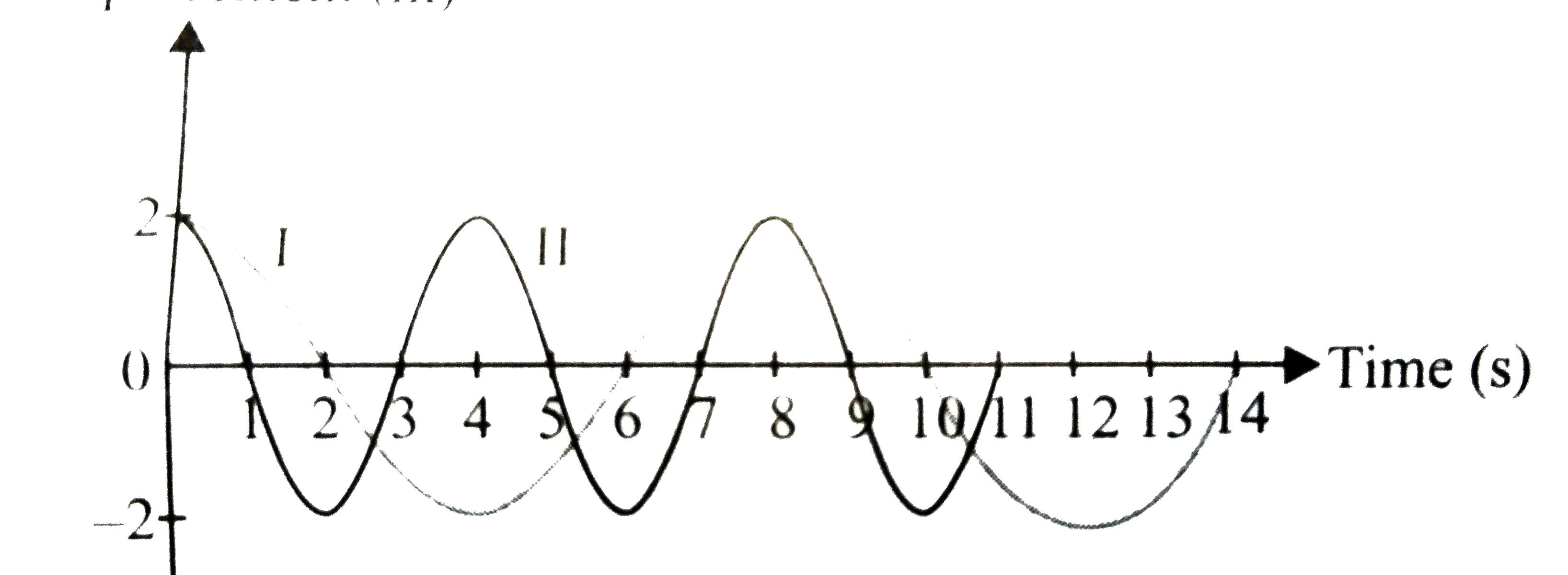
curve I has samme frequency as that of curve II.
curve I has frequency twice that of curve II.
curve I has frequency half that of curve II
curve I has frequency four times that of curve II.
The correct Answer is:C

From the graph
for curve I,
time period, T1=8s, frequency υ1=1T1=18Hz
For curve II,
Time period, T2=4s, frequency, υ2=1T2=14Hz
Their corresponding ratio
υ1υ2=12 or υ1=12υ2.
Topper's Solved these Questions
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Simple Harmonic Motion And Uniform Circular Motion
Explore 3 Videos
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Velocity And Acceleration In Simple Harmonic Motion
Explore 18 Videos
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Simple Harmonic Motion
Explore 17 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTIPSChapter:MOTION IN A STRAIGHT LINEExercise:Assertion And Reason
Explore 15 Videos
- PHYSICAL WORLDBook:NCERT FINGERTIPSChapter:PHYSICAL WORLDExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
Knowledge Check
Figure show the displacement - time graph of a particle moving on the x-axis
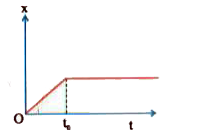 Athe particle is continuously going in positive X directionBthe particle is at restCthe velocity increases up to a time t0 and then becomes constant.Dthe particle moves at constant velocity up to a time t0 and then stops.
Athe particle is continuously going in positive X directionBthe particle is at restCthe velocity increases up to a time t0 and then becomes constant.Dthe particle moves at constant velocity up to a time t0 and then stops.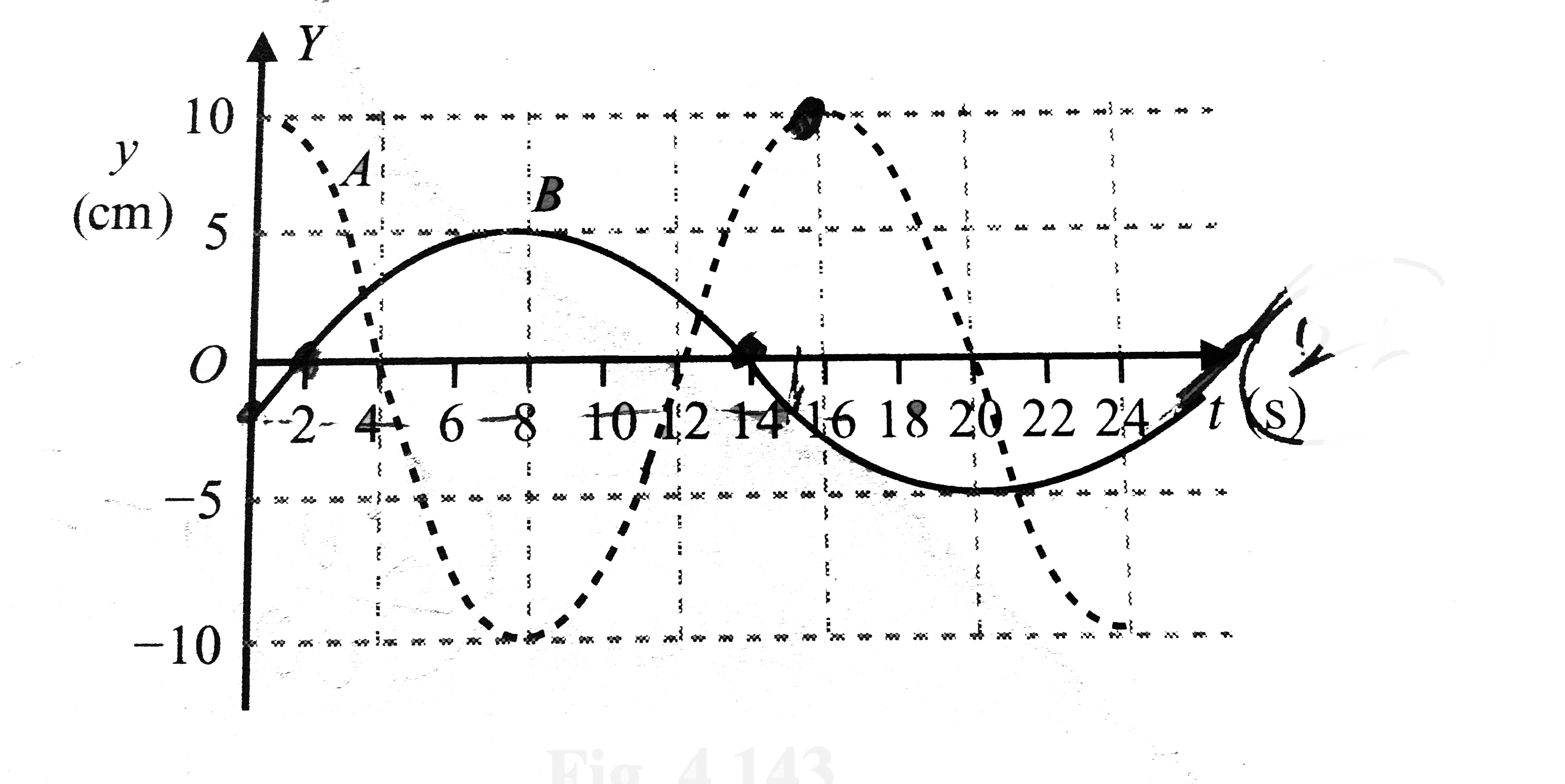
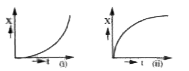
The following figure shows the displacement versus time graph for two particles A and B executing simple harmonic motions. The ratio of their maximum velocities isA3:1B1:3C1:9D9:1Figure (i) and (i) show the displacement-time graphs of two particles moving along the x-axis. We can say that
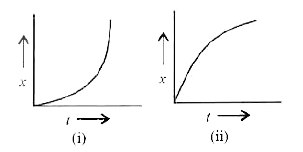 Aboth the particles are having a uniformly retarded motionBboth the particles are having a uniformly acceleraled motionCParticle (1) is having a uniformly accelerated motion while particle (i) is having a uniformly retarded motionDParticle (i) is having a uniformly retarded motion while particle (ii) is having a uniformly accelerated motion
Aboth the particles are having a uniformly retarded motionBboth the particles are having a uniformly acceleraled motionCParticle (1) is having a uniformly accelerated motion while particle (i) is having a uniformly retarded motionDParticle (i) is having a uniformly retarded motion while particle (ii) is having a uniformly accelerated motion
Figure shows the displacement time graph of a particle moving on the X-axis

View Solution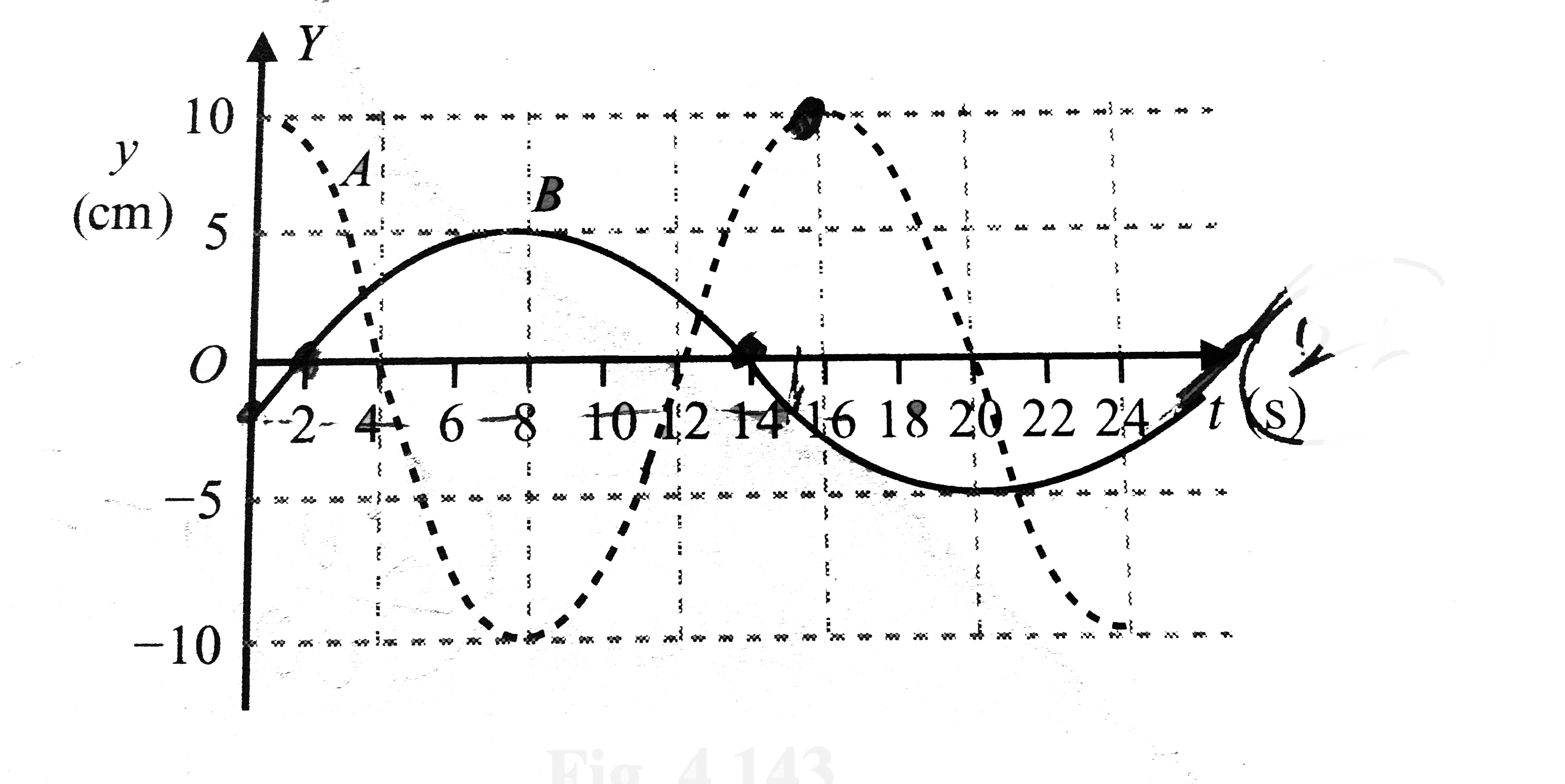
The following figure shows the displacement versus time graph for two particles A and B executing simple harmonic motions. The ratio of their maximum velocities is
View SolutionFigures (i) and (ii) below show the displacement - time graphs of two particles moving along the x-axis. We can say that
View SolutionThe displacement-time graph of a particle executing simple harmonic motion is shown in the figure

Which one of the following graphs is the correct forcetime graph for the motion of the particle ?
View SolutionFigures (i) and (ii) below show the displacement-time graphs of two particles moving along the x -axis. We can say that
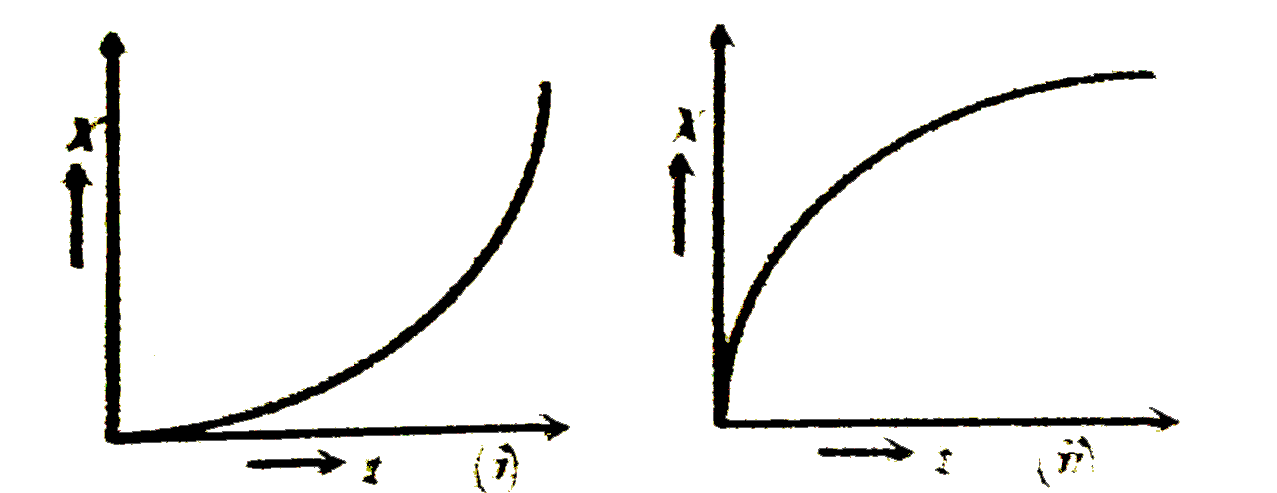
View Solution
