Figure shows three isothermals at temperature T1=4000 K, T2=2000K,T3 = 1000 K.When one mole of an ideal monatomic gas is taken through the paths AB, EC, CD and DA, find the changein internal energy ΔU, the work done by the gas W and the heat Q absorbed by the gas in each path. Also find these quantities for complete cycle ABCDA.
Given VA=1m3 and VB=2m3

(i) When one mole of an ideal gas undergoes a change in temperature ΔT, the change in its internal energy equals CVΔT, where CV is the molar specific heat of the gas at constant volume. For monoatomic gas CV=(3/2) R. Thus the change of internal energy is given by
ΔUAB=CV(TB−TA)
=(3/2)R(4000-2000)=3000R
=3000×8.31=24.93×103 J
ΔUBC=CV(TC−TB)
=(3/2)R(2000-4000)=-3000R
=−24.93×103J
ΔUCD=CV(TD−TC)
=(3/2)R(1000-2000)=-1500R
=−12.465×103 J
ΔUDA=CV(TA−TD)
=(3/2)R(2000-1000)=1500R
=+12.465×103 J
Total ΔU=0
(ii)Workdone by gas during path AB under constant pressure
=P(V2−V1)=R(T1−T2)=8.314×2000
=16.62×103 J
No work is done during BC and DA
Workdone on the gas during CD
=R(T2−T1)=8.314×1000=8.314×103 J
Net workdone by the gas during the cycle
=(16.62×103−8.314×103)=8.314×103 J
(iii) Heat absorbed during
AB=CP(T1−T2)
=Rγγ−1×2000=8.314×(5/3)(5/3)=1×2000
[As γ=5/3 for monoatomic gas ]
=8.314×32×2000=41.55×103 J
Heat released during
BC=CV(T1−T2)
=Rγ−1×2000
=8.314×32×2000=24.93×103J
Heat released during
CD=Rγγ−1×1000
=8.314×52×1000
=20.775×103J
Heat absorbed during
DA=Rγ−1×100
=8.314×32×103J
=12.465×103 J
Net heat absorbed by the gas during the cycle
=(12.465+41.55-20.775-24.93) x 103 J
=8.314×103 J
Topper's Solved these Questions
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Discussion Question
17 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Conceptual MCQs Single Option Correct
21 Videos
- PHOTOELECTRIC EFFECT AND MATTER WAVESBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems
42 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
Similar Questions
One mole of ideal monatomic gas in taken in cyclice process ABCA as shown in the figure

Calculate :
(a) The work done by the gas
(b) The heat rejected by the gas in the path CA
(c) The net heat absorbed be the by gas in the path BC
(d) Maximum temperature obtained by the gas during the cycle.
View Solutionn moles of an ideal gas is taken through a four step cyclic process as shown in the diagram. Calculate work done by the gas in a cycle in terms of temperatures T1,T2,T3 and T4
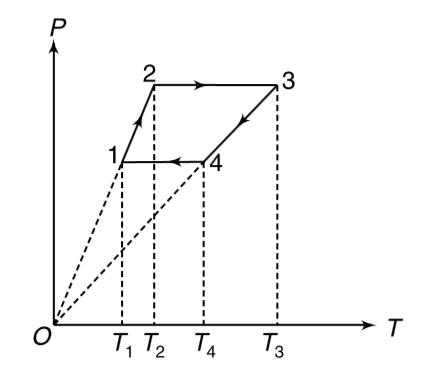
View Solution
Knowledge Check
For one mole of an ideal monoatomic gas, volume and temperature are related as V=KT23. If change in temperature of gas is 90K, then work done is given by W = xR. Find value of x
A60B20C90D30One mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure . Temperature at point 1 =300K and process 2−3 is isothermal .
_S01_113_O01.png) .
.
Net work done by gas in complete cycle isA(9ln3+12)P0V0B(9ln3+4)P0V0C(9ln3−4)P0V0D(9ln3−8)P0V0
The figure shows two isotherms at temperatures T1 and T2. A gas is taken from one isotherm to another isotherm through different processes. Then change in internal energy ΔU has a relation -
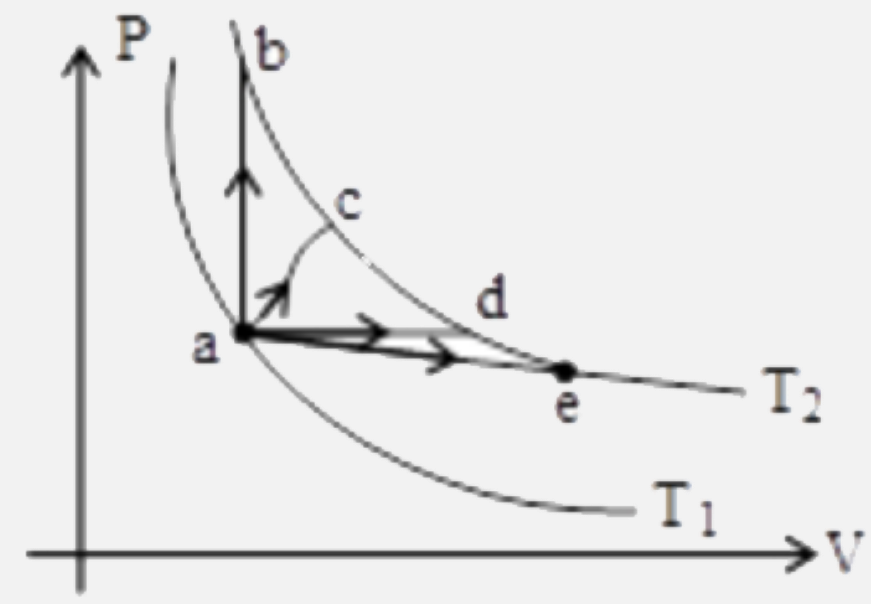
View SolutionThe figure shows two isotherms at temperatures T1 and T2. A gas is taken from one isotherm to another isotherm through different processes. Then change in internal energy ΔU has a relation -

View SolutionOne mole of an ideal gas is heated at constant pressure so that its temperature rises by ΔT= 72 K. In The heat supplied is Q=1.6 kJ, find the change in its internal energy and the work done by the gas.
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure . Temperature at point 1 =300K and process 2−3 is isothermal .
_S01_113_O01.png) .
.
Net work done by gas in complete cycle is
View SolutionI mole of an ideal monoatomic gas is expanded till the temperature of the gas is doubled under the process V2T=contant. The initial temperature of the gas is 400K. In terms of R find total work done in the process.
View SolutionA given mass of gas expands from state A to state B by three paths 1, 2 and 3 as shown in the figure
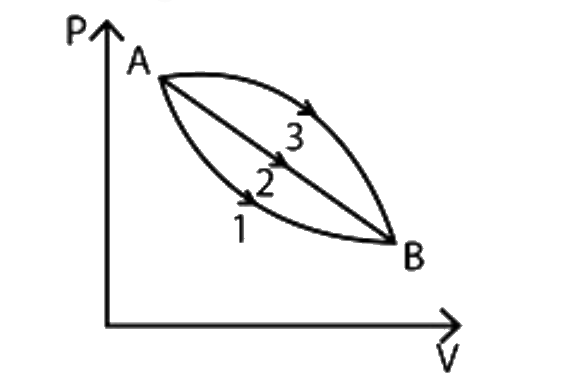
If w1,w2andw3 respectively are be the works done by the gas along three paths, then
View Solution
