Fill water in a beaker or a glass up to its brim. Gently touch the water surface with one of the prongs of the vibrating tuning fork as shown in Fig. 12.2. Now dip the prongs of vibrating tuning fork in water as shown in Fig. 12.3
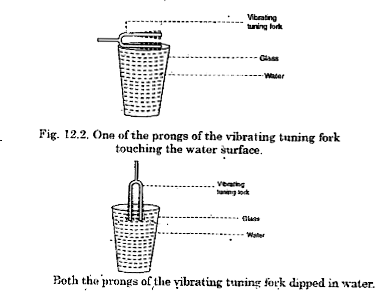
What can you conclude from activity 12.1 and 12.2?
We can conclude that sound cannot be produced without a vibrating body.
Topper's Solved these Questions
Similar Questions
What conclusion can be obtained from the observation that when the prongs of a sound making tuning fork touch the surface of water in a beaker, the water gets splashed?
View SolutionAn object O is placed at a height h = 12 cm above water (μ=43) surface in a beaker . The lower surface of the beaker is polished , as shown in the figure . The location of final image will be
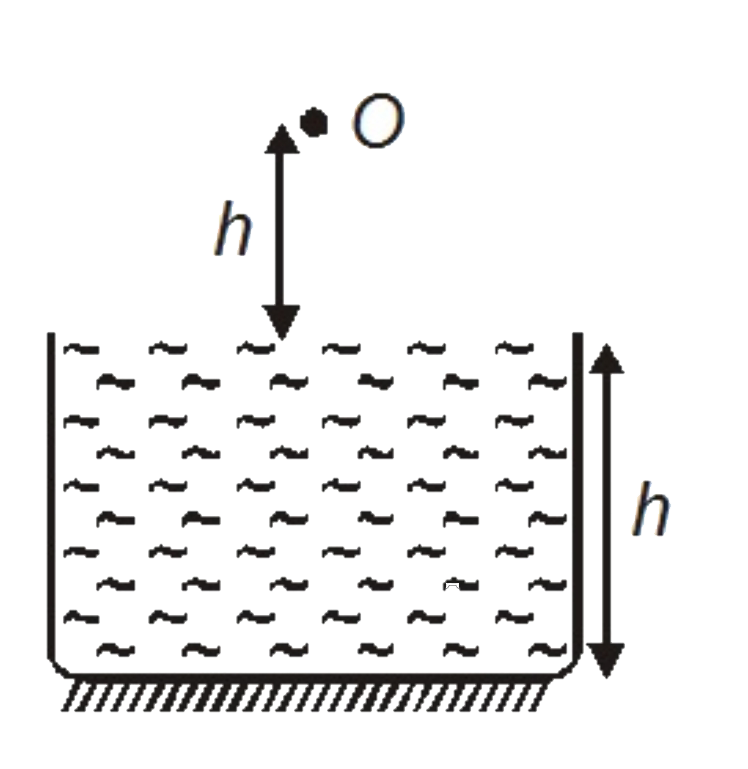
View SolutionAn object O is placed at a height h = 12 cm above water (μ=43) surface in a beaker . The lower surface of the beaker is polished , as shown in the figure . The location of final image will be

View SolutionA glass tube of 1.0m length is filled with water . The water can be drained out slowly at the bottom of the tube . A vibrating tuning fork of frequency 500Hz is brought at the upper end of the tube and the velocity of sound is 330m/s. Find the number of resonances that can be obtained.
View SolutionA glass tube of 1.0m length is filled with water . The water can be drained out slowly at the bottom of the tube . A vibrating tuning fork of frequency 500Hz is brought at the upper end of the tube and the velocity of sound is 330m/s. Find the number of resonances that can be obtained.
View SolutionA U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns Neglect any end effect and assume that the speed of sound in air =330ms−1
View SolutionA U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns Neglect any end effect and assume that the speed of sound in air =330ms−1
View SolutionThe linear mass density of the string shown in the figure is μ=1g/m. One end (A) of the string is tied to a prong of a tuning fork and the other end carries a block of mass M. The length of the string between the tuning fork and the pulley is L=2.0m. When the tuning fork vibrates, the string resonates with it when mass M is either 16 kg or 25 kg. However, standing waves are not observed for any other value of M lying between 16 kg and 25 kg. Assume that end A of the string is practically at rest and calculate the frequency of the fork.

View SolutionA certain fork is found to give 2beats/s when sounded in conjuction with a stretched string vibrating transversely under a tension of either 10.2or9.9kgweight. Calculate the frequency of fork.
View SolutionA tuning fork is found to give 20beatsin12s when sounded in conjuction with a stretched string vibrating under a tension of 10.2or9.9kgf. Calculate the frequency of the fork.
View Solution
