Find an expression fot the magneitc dipole moment and magnetic field induction at the centre of Bohr'r hypothetical hydrogen atom in the n th orbit of the electron in terms of universal constant.
The correct Answer is:B, D
To find the expressions for the magnetic dipole moment and the magnetic field induction at the center of Bohr's hypothetical hydrogen atom in the nth orbit of the electron, we can follow these steps:
Step 1: Magnetic Dipole Moment Calculation
1. Formula for Magnetic Dipole Moment (μ):
The magnetic dipole moment for an electron in the nth orbit can be expressed as:
μn=I⋅A
where I is the current and A is the area of the orbit.
2. Current (I) in nth Orbit:
The current I can be defined as the charge Q passing through the orbit per unit time. The time period Tn for one complete revolution of the electron in the nth orbit is given by:
I=QTn
3. Area (A) of nth Orbit:
The area A of the circular orbit is:
A=πR2n
where Rn is the radius of the nth orbit.
4. Substituting for Current and Area:
Therefore, the magnetic dipole moment can be rewritten as:
μn=(QTn)⋅(πR2n)
5. Finding the Time Period (T_n):
The time period Tn can be expressed in terms of angular velocity (ωn):
Tn=2πωn
Thus, we can substitute this into the current expression:
I=Q⋅ωn2π
6. Final Expression for Magnetic Dipole Moment:
Substituting I back into the expression for μn:
μn=Q⋅ωn2π⋅πR2n=Q⋅ωn⋅R2n2
7. Expressing in Terms of Constants:
Using the relationships Vn=Ze2n and Rn=R0n2Z, we can simplify further:
μn=Q⋅Vn⋅Rn2
This leads to:
μn=Q⋅V0⋅R02⋅n
where V0 and R0 are constants.
Step 2: Magnetic Field Induction Calculation
1. Formula for Magnetic Field (B):
The magnetic field induction at the center of the atom due to the revolving electron is given by:
Bn=μ0In2Rn
2. Substituting for Current (I_n):
Using the expression for current In:
Bn=μ0⋅QTn2Rn
3. Substituting for Time Period (T_n):
Substitute Tn in the expression:
Bn=μ0⋅Q⋅ωn4πRn
4. Final Expression for Magnetic Field:
Substituting Rn and simplifying:
Bn=μ0QV0Z34πR20n5
This can be expressed as:
Bn=B0Z3n5
where B0 is a constant.
Summary of Results
- Magnetic Dipole Moment:
μn=QV0R02n
- Magnetic Field Induction:
Bn=B0Z3n5
The magnetic dipole moment for an electron in the nth orbit can be expressed as:
μn=I⋅A
where I is the current and A is the area of the orbit.
The current I can be defined as the charge Q passing through the orbit per unit time. The time period Tn for one complete revolution of the electron in the nth orbit is given by:
I=QTn
The area A of the circular orbit is:
A=πR2n
where Rn is the radius of the nth orbit.
Therefore, the magnetic dipole moment can be rewritten as:
μn=(QTn)⋅(πR2n)
The time period Tn can be expressed in terms of angular velocity (ωn):
Tn=2πωn
Thus, we can substitute this into the current expression:
I=Q⋅ωn2π
Substituting I back into the expression for μn:
μn=Q⋅ωn2π⋅πR2n=Q⋅ωn⋅R2n2
Using the relationships Vn=Ze2n and Rn=R0n2Z, we can simplify further:
μn=Q⋅Vn⋅Rn2
This leads to:
μn=Q⋅V0⋅R02⋅n
where V0 and R0 are constants.
The magnetic field induction at the center of the atom due to the revolving electron is given by:
Bn=μ0In2Rn
Using the expression for current In:
Bn=μ0⋅QTn2Rn
Substitute Tn in the expression:
Bn=μ0⋅Q⋅ωn4πRn
Substituting Rn and simplifying:
Bn=μ0QV0Z34πR20n5
This can be expressed as:
Bn=B0Z3n5
where B0 is a constant.
- Magnetic Dipole Moment:
μn=QV0R02n
- Magnetic Field Induction:
Bn=B0Z3n5
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Passage 4
1 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
Find an expression for the magnetic dipole moment and magnetic field induction at the center of Bohr's hypothetical hydrogen atom in the nth orbit of the electron in terms of universal constant.
View SolutionDeduce an expression for the magnetic dipole moment of an electron orbiting around the central nucleus.
View SolutionThe magnetic field induction produced at the centre of orbit due to an electron revolving in nth orbit of hydrogen atom is proportional to
View SolutionThe ratio of magnetic dipole moment of an electron of charge e and mass m in the Bohr orbit in hydrogen to the angular momentum of the electron in the orbit is:
View SolutionAccording to Bohr model, magnetic field at the centre (at the nucleus) of a hydrogen atom due to the motion of the electron in nth orbit is proportional to 1/nx, find the value of x
View SolutionMagnetic field at the center (at nucleus) of the hydrogen like atom (atomic number=z) due to the motion of electron in nth orbit is proporional to
View SolutionMagnetic moment of an electron in nth orbit of hydrogen atom is
View SolutionMagnetic moment of an electron in nth orbit of hydrogen atom is
View SolutionCalculate the value of X if magnetic field strength at the centre of a hydrogen atom caused by an electron moving along the first Bohr orbits is X2T.
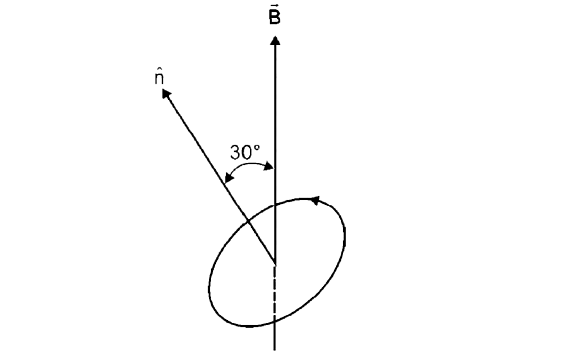
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.
View Solution
