Find coordinates of mass center of a semicircular ring of radius r placed symmeric to the y-axis of a Cartesian coordinate system.
The axis is the line of symmetry, therefore mass center of the ring lies on it making x-cordinate zero. Distance OC of mass center from center is given by the result obtained in example 4. Making use of this result, we have
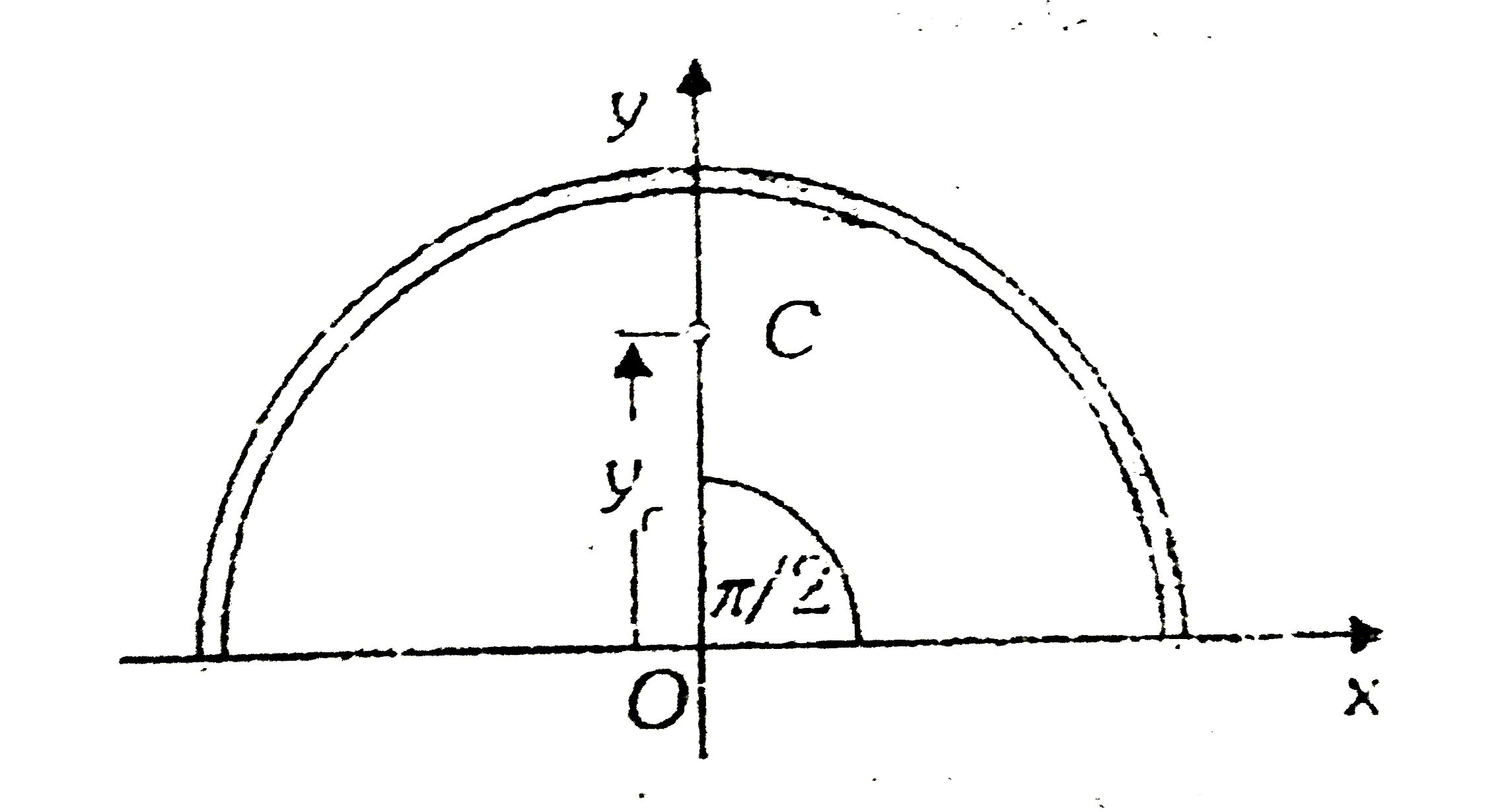
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Find coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.
View SolutionFind coordinates of mass center of a quarter ring of radius r placed in the first quadrant of a Cartesian coordinate system, with centre at origin.
View Solution
Knowledge Check
Three thin uniform rods each of mass M and length L and placed along the three axis of a Cartesian coordinate system with one end of each rod at the origin. The M.I. of the system about z-axis is
AML23B2ML23CML26DML2Three thin uniform rods each of mass M and length L and placed along the three axis of a Cartesian coordinate system with one end of each rod at the origin. The M.I. of the system about z-axis is
AML23B2ML23C2ML26DML2Three thin uniform rods each of mass M and length L are placed along the three axes of a cartesian coordinate system. The moment of inertia of the system about z-axis is
Aml23B2ML23CML26DML2
Find coordinates of mass center of a quarter sector of a uniform disk of radius r placed in the first quadrant ofa Cartesian coordinate system with centre at origin.
View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionFind the centre of mass of a homogeneous semicircular plate of radius a.
View SolutionFind the coordination of the centre of mass of a uniform semicircular wire of radius R and mass M.
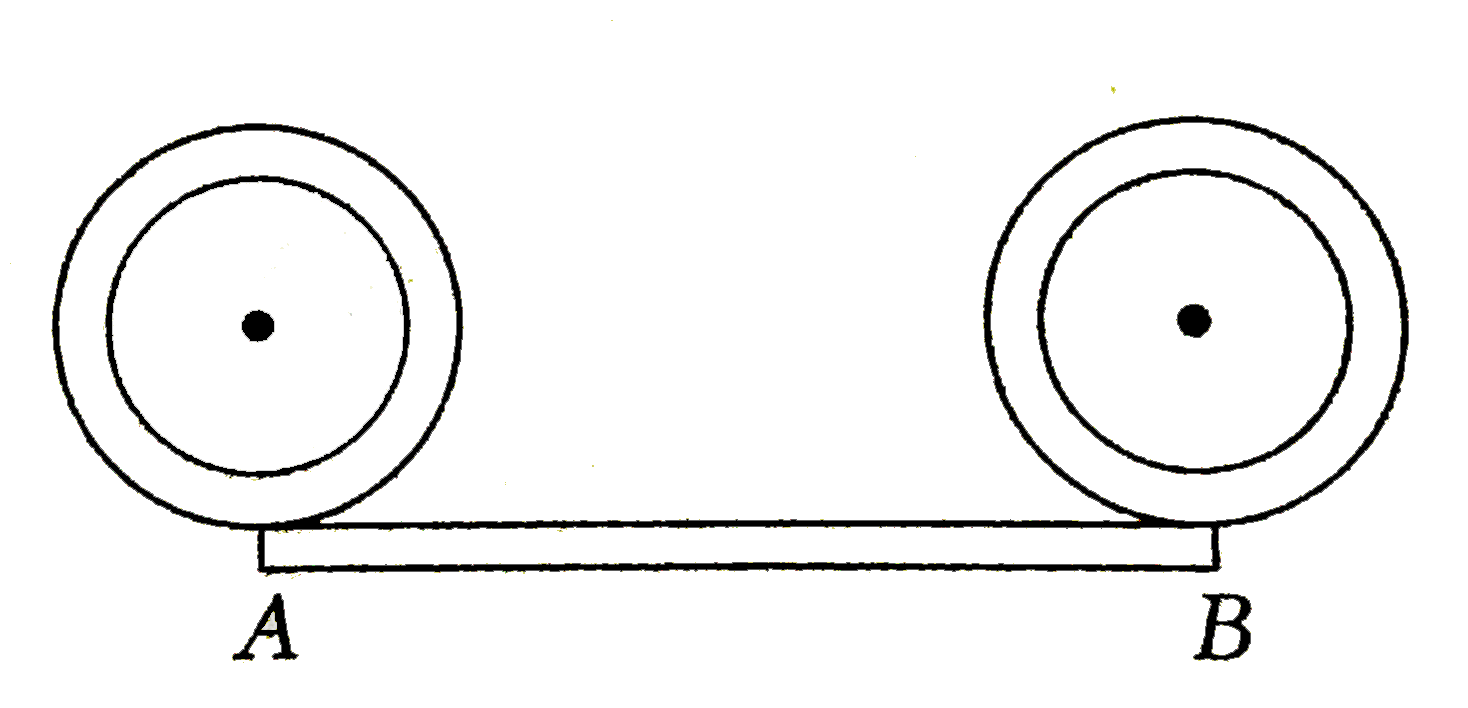
View SolutionYou are supplied with three identical rods of same length and mass. If the length of each rod is 2π. Two of them are converted into rings and then placed over the third rod as shown in figure. If point A is considered as origin of the coordinate system the coordinate of the center of mass will be (you may assume AB as x-axis of the coordinate system).
View Solution
