Find moment of inertia of half disc of radius R2 and mass M about its centre. A smaller half disc of radius R1 is cut from this disc
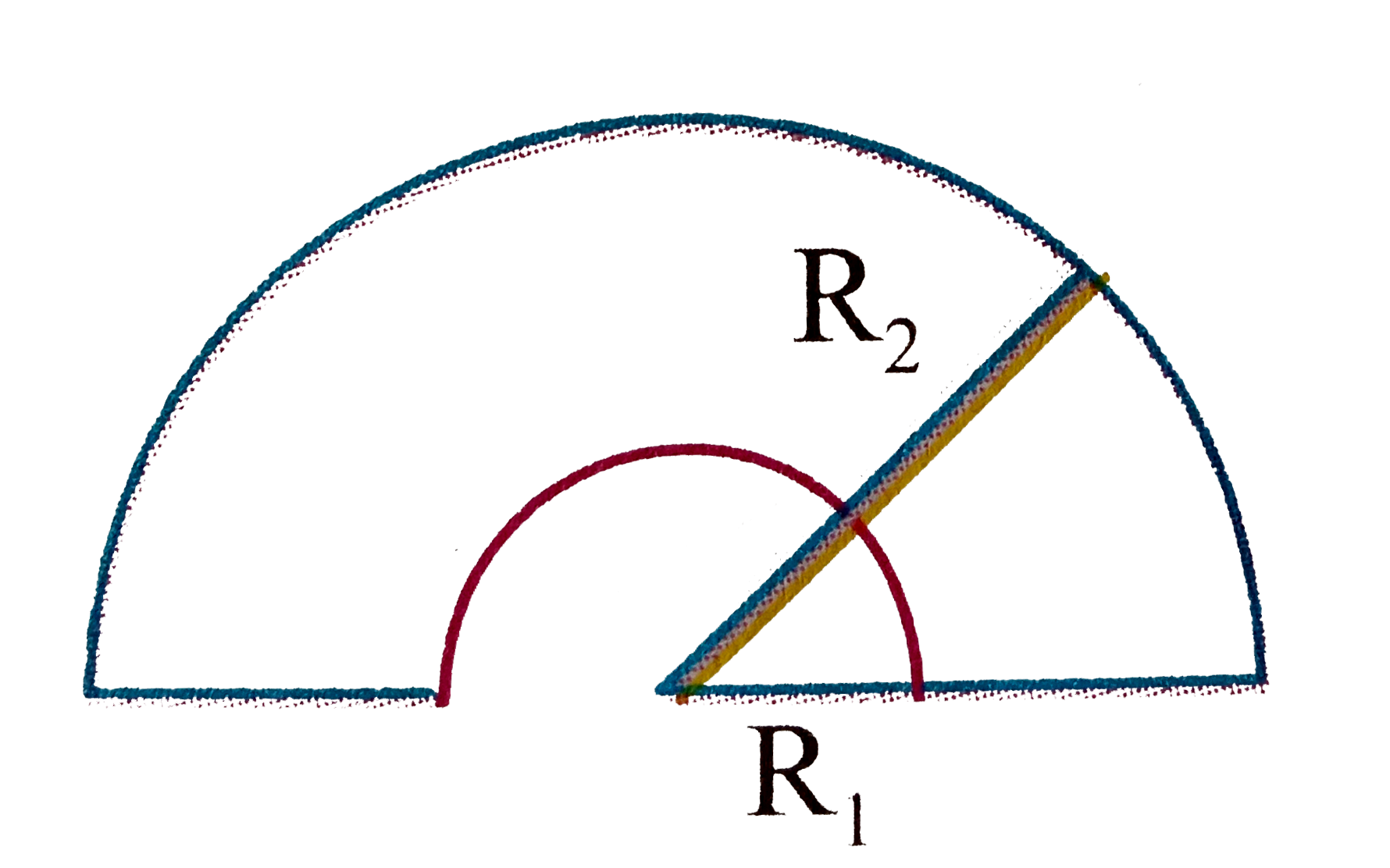
Step by step video & image solution for Find moment of inertia of half disc of radius R_2 and mass M about its centre. A smaller half disc of radius R_1 is cut from this disc by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Practive Exercise
28 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Discussio Q
28 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
Knowledge Check
Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
AMR22BMR24CMR23DMR212The moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
A23MR2B32MR2C45MR2D54MR2The moment of inertia of a solid sphere of radius R about its diameter is same as the that of disc of radius 2R about its diameter. The ratio of their masses is -
A5:2B5:8C4:1D2:1
The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is
View SolutionThe moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is.
View SolutionThe moment of inertia of a solid sphere of radius R about its diameter is same as that of a disc of radius 2R about its diameter. The ratio of their masses is
View SolutionThe moment of inertia of a solid sphere of radius R about its diameter is same as that of a disc of radius 2R about its diameter. The ratio of their masses is
View SolutionThe moment of inertia of a thin circular disc of mass M and radius R about any diameter is
View Solution
