Find out the coefficient of linear expansion of the material of an open pipe so that the frequency of any tone emitted from it does not very with temperature .
The fundamental frequencies at 0∘ C and t∘ C are respectively ,
n1=V02l0andn2Vt2lt
Here, V0 = velocity of sound at 0∘Cl0 = length of the pipe at 0∘C,Vt = velocity of sound at t∘C,lt = length of the pipe at t∘C .
According to the question, n1=n2
so , V02l0=Vt2lt
or , V0lt=Vtl0orV0l0(1+αt)=V0(1+0.00183t)l0
[α= coefficient of linear expansion]
or, α=0.00183∘C−1 .
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Higher order thinking skill (hots) questions
21 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Multiple choice questions (Based on standing wave)
5 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - CBSE SCANNER
3 Videos
- THERMOMETRYBOOK - CHHAYA PUBLICATIONCHAPTER - THERMOMETRYEXERCISE - EXAMINATION ARCHIEVE - WBJEE
1 Videos
Similar Questions
If the coefficient of linear expansion of a material is high, the material will expand more for each degree rise in temperature
View SolutionA parallel plate capacitor of area A and separation d is provided with thin insulating spacers to keep its plates aligned in an environment of fluctuating temperature. If the coefficient of thermal expansion of material of the plate is α, find the coefficient of thernal expansion (αs) of the spacers in order that the capacitance does not vary with temperature. (Ignore effect of the spacers on capacitance.)
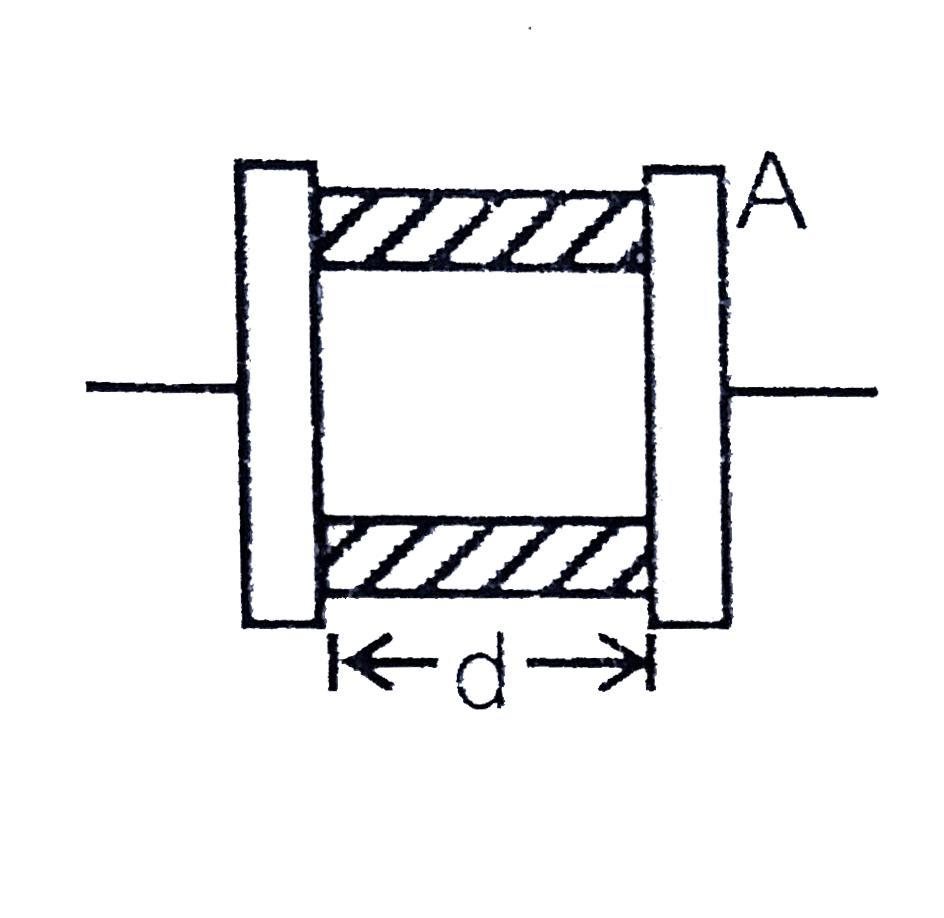
View Solution
Knowledge Check
The radius of metal sphere at room temperature T is R and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature T, so that new temperature is T+ΔT. The increase in volume of sphere is approximately
A2πRαΔTBπR2αΔTC4πR3αΔT3D4πR2αΔTThe radius of metal sphere at room temperature T is R and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature T, so that new temperature is T+ΔT. The increase in volume of sphere is approximately
A2πRαΔTBπR2αΔTC4πR3αΔT/3D4πR3αΔTA parallel plate capacitor of area A and separation d is provided with thin insulating spacers to keep its plates aligned in an environment of fluctuating temperature. If the coefficient of thermal expansion of material of the plate is α, find the coefficient of thernal expansion (αs) of the spacers in order that the capacitance does not vary with temperature. (Ignore effect of the spacers on capacitance.)
 Aαs=α2Bαs=3αCαs=2αDαs=α
Aαs=α2Bαs=3αCαs=2αDαs=α
A fluid having a thermal coefficient of volume expansion γ is filled in a cylindrical vessel up to a height h0. The coefficient of linear thermal expansion of the material of the vessel is α . If the fluid is heated with the vessel , then find the level of liquid when temperature increases by Δθ.
View SolutionThe fundamental frequency of an organ pipe is independent of small variation in temperature. The coefficient of linear expansion of the material is α. The temperature of the tube at this instant is Nα. The value of N is ………
View SolutionImagine a hypothetical material whose average temperature coefficient of linear expansion is 0.1/.∘C .Find the fractional increase in area of thin square plate of above material when temperature is increase by 10∘C
View SolutionImagine a hypothetical material whose average temperature coefficient of linear expansion is 0.1/.∘C .Find the fractional increase in area of thin square plate of above material when temperature is increase by 10∘C
View SolutionA fluid having a thermal coefficient of volume expansion γ is filled in a cylindrical vessel up to a height h0. The coefficient of linear thermal expansion of the material of the vessel is α . If the fluid is heated with the vessel , then find the level of liquid when temperature increases by Δθ.
View Solution
