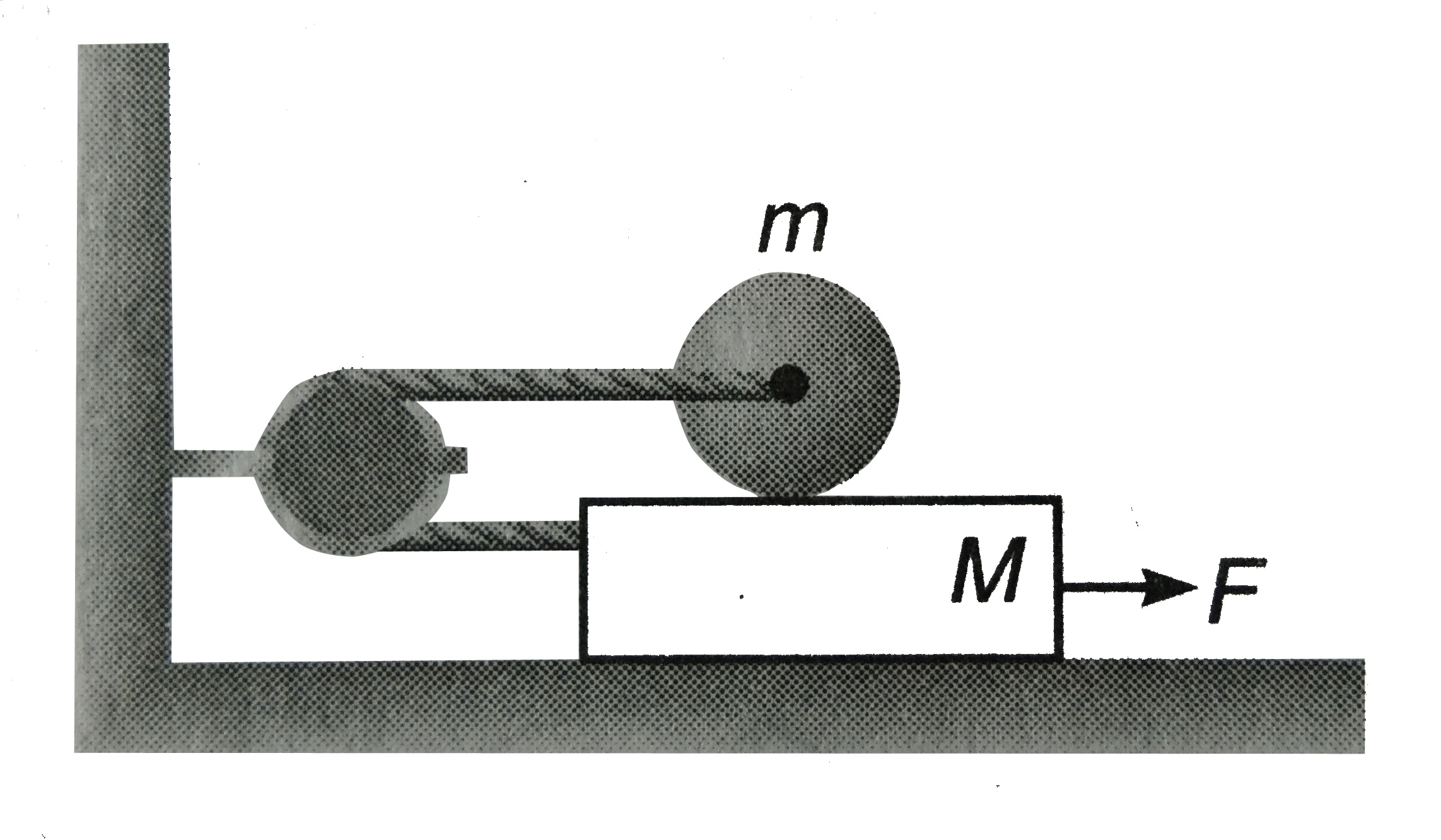
Find the acceleration of the cylinder of mass m and radius R and that of plank of mass M placed on smooth surface if pulled with a force F as shown in figure. Given that sufficient friction is present between cylinder and the plank surface to prevent sliding of cylinder.
F−T−f=Ma……i
T−f=Ma…………ii
α=fR12mR2=2fmR…….iii
Constraint relation aplank=aP
Rα−a=a
or Rα=2a……iv

Solving these equations, we get
a=F3m+M
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.2
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Find the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionA uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is

View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA cylinder of mass M and radius R is to be raised on a horizontal step of height h=R3. Cylinder is pulled by a rope as shown in figure. Assuming no slipping, the minimum value of force F to raise the cylinder is
_PHY_E05_246_Q01.png)
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is
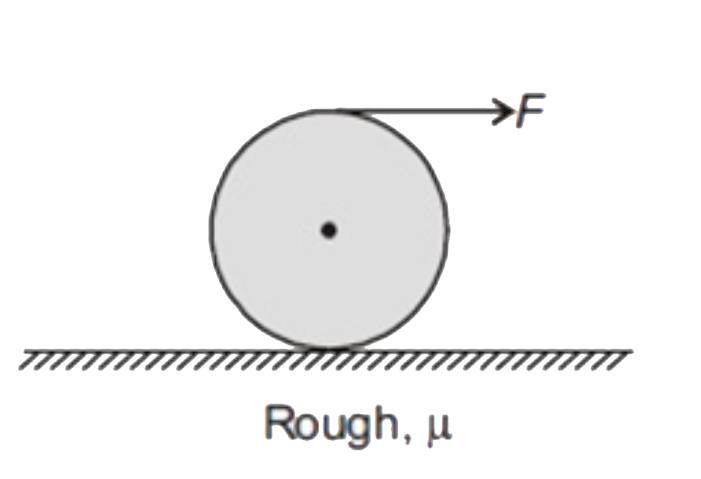
View SolutionA disc of radius R and mass M is under pure rolling under the action of a force F applied at the topmost point as shown in figure. There is sufficient friciton between the disc and the horizontal surface. The acceleration is given as

View SolutionConsider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc

View SolutionA thin but very large plank of mass 2 m is placed on a horziontal smooth surface. A solid cylinder of mass m and radius r is given only translational velocity v0 and gently placed on the plank as shown in the figure. The coefficient of kinetic friciton between the plank and the cylinder is μ.
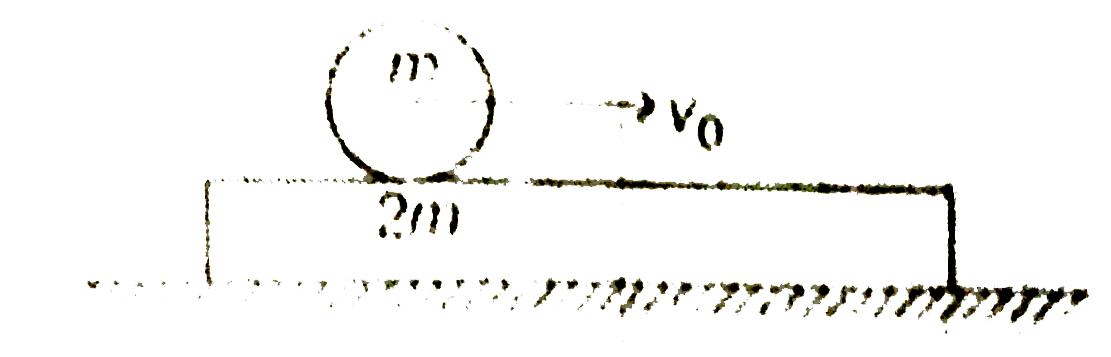
the cylinder given impluse t=0, than at what time pure rolling starts
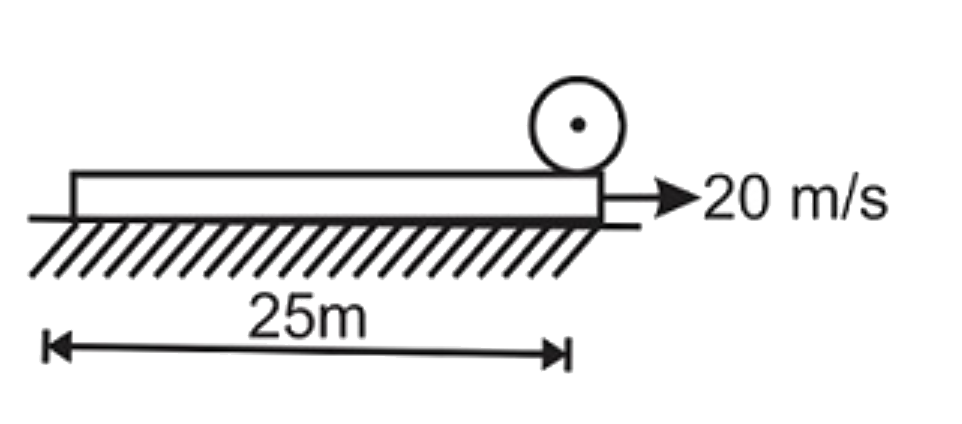
View SolutionA solid cylinder is kept on one edge of a plank of same mass and length 25 m placed on a smooth surface as shown in the figure. The coefficient of friction between the cylinder and the plank is 0.5. The plank is given a velocity of 20ms−1 towards right. Find the time (in S) after which plank any cylinder will separate. [g=10ms−2]
View Solution
