Find the angle between the diagonals of a cube with edges of length "a".
Video Solution
Text Solution
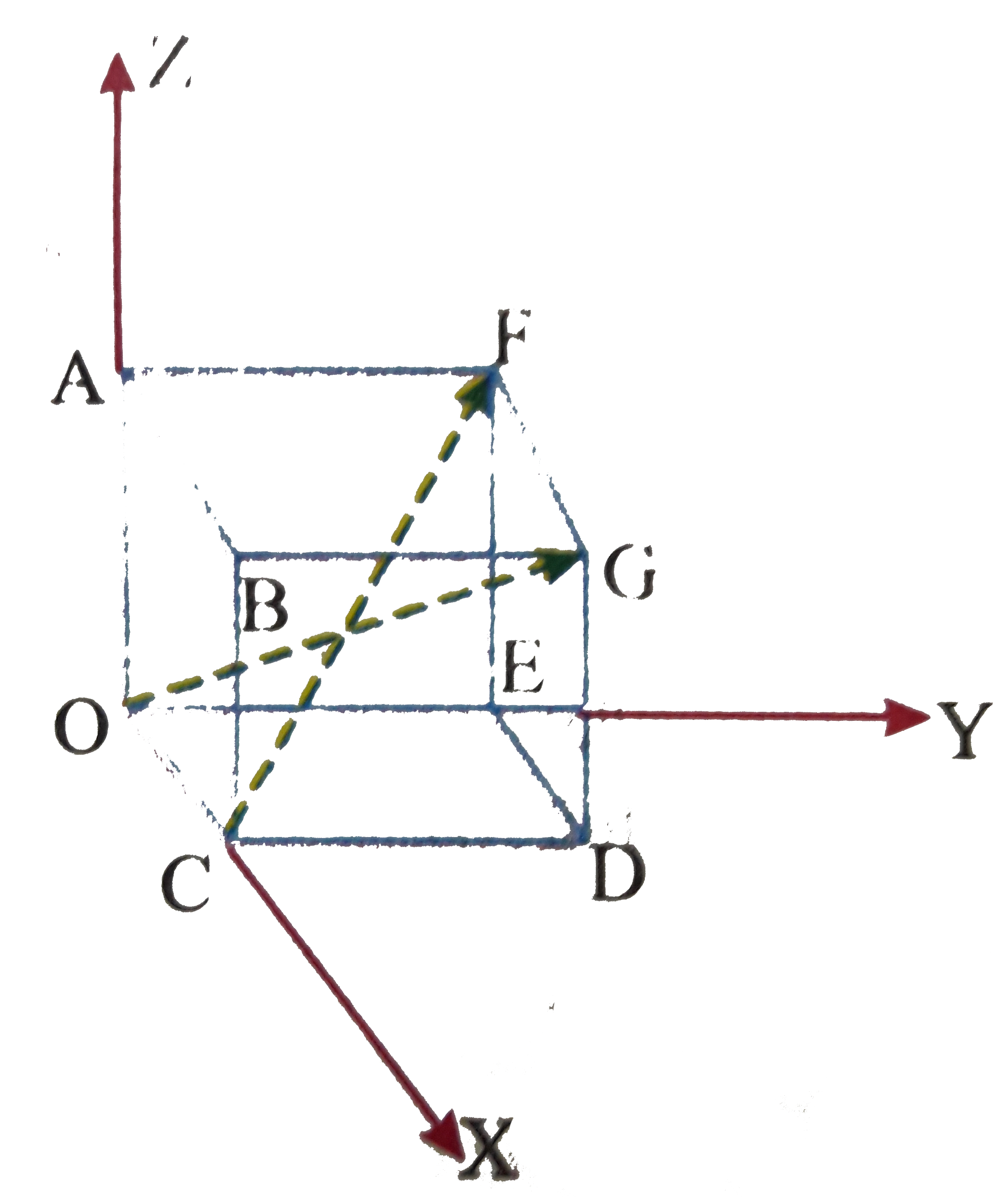
From the diagram
¯¯¯¯¯¯OG=¯¯¯¯d1=αˆi+αˆj+αˆk,¯¯¯¯¯¯CF=¯¯¯¯d2=−αˆi+αˆj+αˆk
∴ The angle angle between the diagonals is
cosθ=→d1.→d2∣∣→d1∣∣.∣∣→d2∣∣=13⇒θ=cos−1(13)
|
Topper's Solved these Questions
- VECTORSBOOK - NARAYNACHAPTER - VECTORSEXERCISE - C.U.Q
34 Videos
- VECTORSBOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-I (C.W)
27 Videos
- UNITS AND MEASUREMENTSBOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION
23 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-IV
56 Videos
Similar Questions
Knowledge Check
The angle between two diagonals of a cube İs
Acos−1(13)B30∘Ccos−1(1√3)D45∘The angle between two diagonals of a cube will be
Asin−1(13)Bcos−1(13)CvariableDnone of theseThe angle between two diagonals of a cube will be
Asin−1(13)Bcos−1(13)CvariableDnone of these
Find the angel between any two diagonals of a cube.
View SolutionCosine of the angle between two diagonals of a cube is equal to :
View SolutionCosine of the angle between two diagonals of a cube is equal to :
View SolutionIf θ is the acute angle between the diagonals of a cube then which one of the following is correct
View SolutionThe angle between a diagonal of a cube and one of its edges is
View Solution
