Find the angular momentum of a disc about the axis shown in figure in the following situations.

Video Solution

Text Solution

Verified by Experts

Case a: In this case the disc is rotating about fixed axis which is parallel to the $z$ -axis.
$H e n c e \vec{L} = I_{z} (\hat{k}) = (\frac{M R^{2}}{2}) ω (\hat{k})$
direction can be determined using right hand rule.
Case b: In this case also the disc rotates about fixed axis. We can write angular momentum for this situation.
$\vec{L} = I_{z} ω (\hat{k})$
Uisnng parallel axis we can find the value of $I_{2} = \frac{M R^{2}}{2} + M d^{2}$ Hence $\vec{L} = (\frac{M R^{2}}{2} + M d^{2}) ω (\hat{k})$
Case c: In this case the disc is rotating about an axis parallel to the $z$ -axis and centre of disc is also translating.
Hence, angular momentum,
$\vec{L} = I_{c m} \vec{ω} + \vec{r} \times m \vec{v}$
$= \frac{M R^{2}}{2} ω (- \hat{k}) + M v d (- \hat{k})$
$= (\frac{M R^{2}}{2} ω + M v d) (- \hat{k})$
Case d: In the case also the the disc is rotating about an axis passing through it centre and parallel to $y$ -axis and centre of mass of disc is translating with velocity $v$ parallel to $x$ -axis
$\vec{L} = I_{C M} ω (\hat{j}) + M v d (\hat{k})$
Here $I_{C M} = \frac{M R^{2}}{4}$
Hence , $\vec{L} = \frac{M R^{2}}{4} ω (\hat{j}) + M v d (\hat{k})$

Updated on:21/07/2023

A disc of mass M and radius R is rolling with angular speed $ω$ on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
A $(1 / 2) M R^{2} ω$
B $M R^{2} ω$
C $(3 / 2) M R^{2} ω$
D $2 M R^{2} ω$
A disc of mass $m$ and radius $R$ moves in the $x - y$ plane as shown in Fig. The angular momentum of the disc about the origin $O$ at the instant shown is

A $- \frac{5}{2} m R^{2} ω ˆ k$
B $\frac{7}{3} m R^{2} ω ˆ k$
C $- \frac{9}{2} m R^{2} ω ˆ k$
D $\frac{5}{2} m R^{2} ω ˆ k$
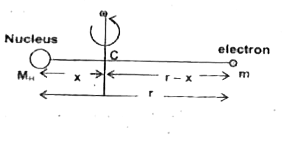
The angular momentum of the atom will be constant about an axis passing through
Anucleus
Belectron
Ccentre of mass of the atom
Dany axis perpendicular to the line joining the electron and nucleus