Find the capacitance of the capacitor shown in the figure. Area of AB is A. are dielectric constants of respective materials

Here and are in parallel . Their equivalent capacitance is

Now capacitor with dielectric is series with . If equivalent capacitance of whole system is C then
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B (questions)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section C ( NCERT Exemplar Solution ) ( Multiple Choice Questions (MCQs ) )
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B ( Numerical From Textual Exercise )
46 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION D Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams) MCQs asked in Board Exam and GUJCET
7 Videos
Similar Questions
A parallel plate capacitor is of area 6 cm2 and a separation 3 mm. The gap is filled with three dielectric materials of equal thickness (see figure) with dielectric constant K1=10, K2=12andK3=14. The dielectric constant of a material which when fully inserted in above capacitor, gives same capacitance would be :
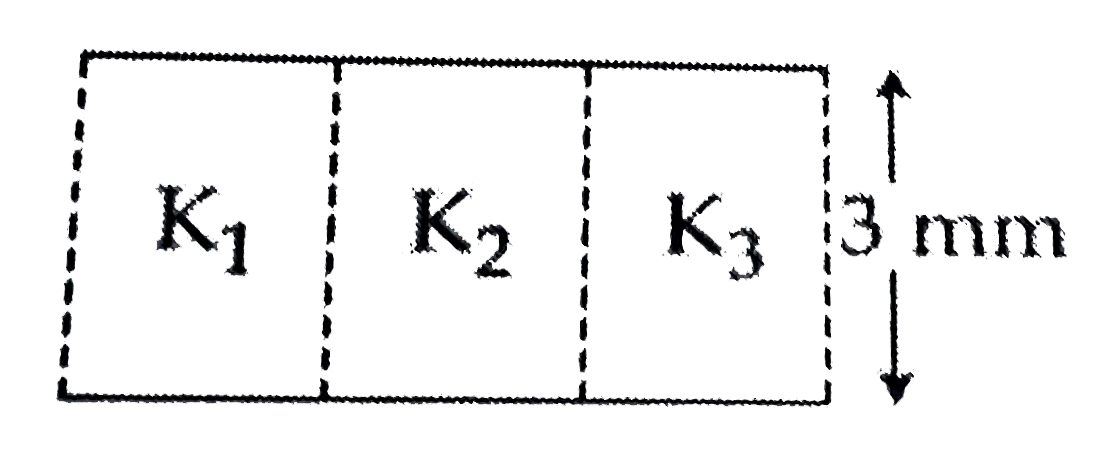
View SolutionA parallel plate capacitor is of area 6 cm2 and a separation 3 mm. The gap is filled with three dielectric materials of equal thickness (see figure) with dielectric constant K1=10, K2=12andK3=14. The dielectric constant of a material which when fully inserted in above capacitor, gives same capacitance would be :
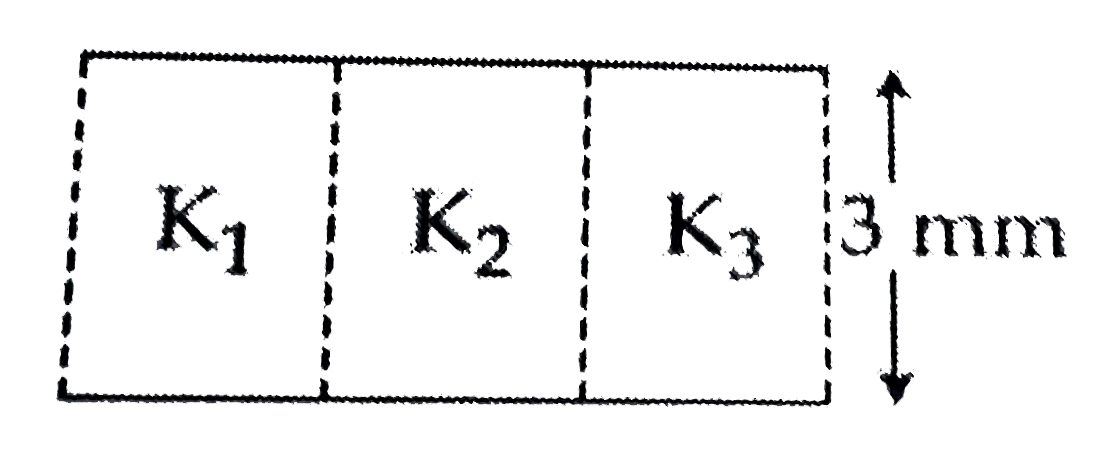
View Solution
Knowledge Check
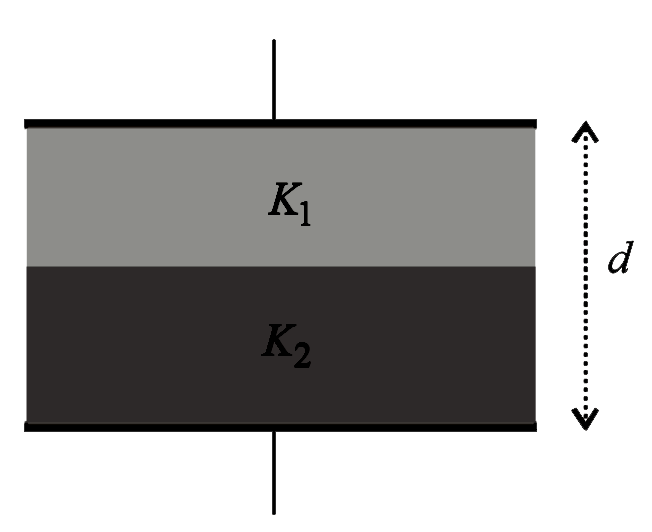
The capacitance of a capacitor, filled with two dielectrics of same dimensions but of dielectric constants K1andK2 respectively as shown will be -
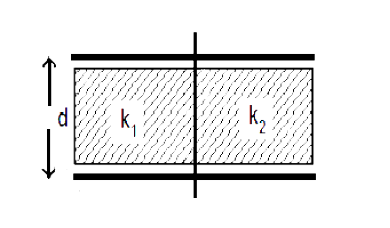 A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)
A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)The space between the plates of a parallel plate capacitor of capacitance C is filled with three dielectric slabs of identical siza as shown in figure. If the dielectric constants of the three slabs are K1,K2andK3 find the new capacitance.
 ACeq=(K1+K2+K3)C3BCeq=(K1−K2+K3)C3CCeq=(K1+K2−K3)C3DCeq=(K1−K2−K3)C3
ACeq=(K1+K2+K3)C3BCeq=(K1−K2+K3)C3CCeq=(K1+K2−K3)C3DCeq=(K1−K2−K3)C3
In the figure a capacitor is filled with dielectrics K1,K2 and K3. The resultant capacitance is
View SolutionIn the figure a capacitor is filled with dielectrics K1,K2 and K3. The resultant capacitance is

View SolutionThe space between the plates of a parallel plate capacitor of capacitance C is filled with three dielectric slabs of identical size as shown in figure. If the dielectric constants of the three slabs are K1,K2andK3 find the new capacitance.

View SolutionTwo identical capacitors of plate dimensions: l×b and plate separation d have dielectric slabs filled in between the space of the plates as shown in the figures. if capacitance of both capacitor is same, Obtain the relation between the dielectric constant K,K1andK2.
View SolutionFind the capacitance of a system of three parallel plates, each of area A metre2 separated by distances d1andd2 metre respectively. The space between them is filled with dielectrics fo relatives dielectric constants K1andK2. The dielectric constant of free space is ∈0.
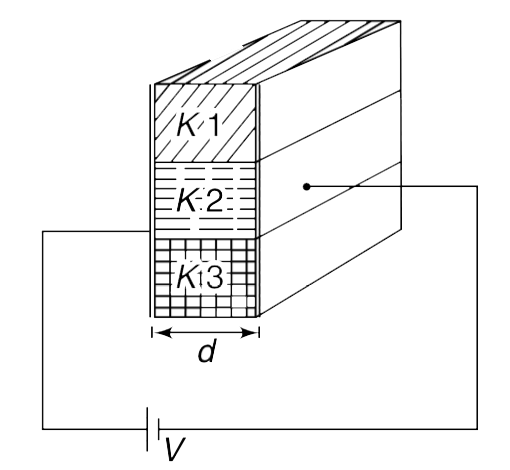
View SolutionA parallel plate capacitor of plate area A and spac- ing between the plates d is filled with three dielectrics as shown in the Figure. The dielectric constants of the three dielectrics are K1=K,K2=2K,K3=3K. The capacitor is connected to a cell of emf V.
(a) Write the ratio of maximum to minimum charge density on the surface of the capacitor plate.
(b) Calculate the surface charge density of bound (induced) charge on the middle dielectric.
(c) If the three dielectrics occupy equal volume between the plates, calculate the capacitance of the capacitor.
View Solution
