Find the components of weight along and perpendicular to a plane if a mass of 4 kg is laying on the plane making an angle making an angle of 60∘ with the horizontal .
The correct Answer is:33.948N,19.6N
To find the components of weight along and perpendicular to a plane for a mass of 4 kg resting on an inclined plane at an angle of 60 degrees with the horizontal, we can follow these steps:
Step 1: Calculate the Weight of the Mass
The weight (W) of the mass can be calculated using the formula:
W=m⋅g
where:
- m=4kg (mass)
- g=10m/s2 (acceleration due to gravity)
Calculating the weight:
W=4kg⋅10m/s2=40N
Step 2: Identify the Angle of Incline
The angle of the incline with the horizontal is given as θ=60∘.
Step 3: Calculate the Component of Weight Perpendicular to the Plane
The component of the weight perpendicular to the incline (W_perpendicular) can be calculated using the cosine of the angle:
W_{\perpendicular} = W \cdot \cos(\theta)
Substituting the values:
W_{\perpendicular} = 40 \, \text{N} \cdot \cos(60^\circ)
Since cos(60∘)=12:
W_{\perpendicular} = 40 \, \text{N} \cdot \frac{1}{2} = 20 \, \text{N}
Step 4: Calculate the Component of Weight Along the Plane
The component of the weight along the incline (W_parallel) can be calculated using the sine of the angle:
W∥=W⋅sin(θ)
Substituting the values:
W∥=40N⋅sin(60∘)
Since sin(60∘)=√32:
W∥=40N⋅√32=20√3N
Final Results
- The component of weight perpendicular to the plane is W_{\perpendicular} = 20 \, \text{N} .
- The component of weight along the plane is W∥=20√3N.
The weight (W) of the mass can be calculated using the formula:
W=m⋅g
where:
- m=4kg (mass)
- g=10m/s2 (acceleration due to gravity)
W=4kg⋅10m/s2=40N
The angle of the incline with the horizontal is given as θ=60∘.
The component of the weight perpendicular to the incline (W_perpendicular) can be calculated using the cosine of the angle:
W_{\perpendicular} = W \cdot \cos(\theta)
Substituting the values:
W_{\perpendicular} = 40 \, \text{N} \cdot \cos(60^\circ)
W_{\perpendicular} = 40 \, \text{N} \cdot \frac{1}{2} = 20 \, \text{N}
The component of the weight along the incline (W_parallel) can be calculated using the sine of the angle:
W∥=W⋅sin(θ)
Substituting the values:
W∥=40N⋅sin(60∘)
W∥=40N⋅√32=20√3N
- The component of weight perpendicular to the plane is W_{\perpendicular} = 20 \, \text{N} .
- The component of weight along the plane is W∥=20√3N.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS (2)
9 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS (3)
2 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
Knowledge Check
A person pushes a block of mass 4 kg up a frictionless inclined plane 10 m long and that makes an angle of 30∘ with the horizontal . Then the work done is
A33.5JB−392JC339.4JD−196JA particle is thrown at time t=0 with a velocity of 10 m/s at an angle of 60∘ with the horizontal from a point on an incline plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is :
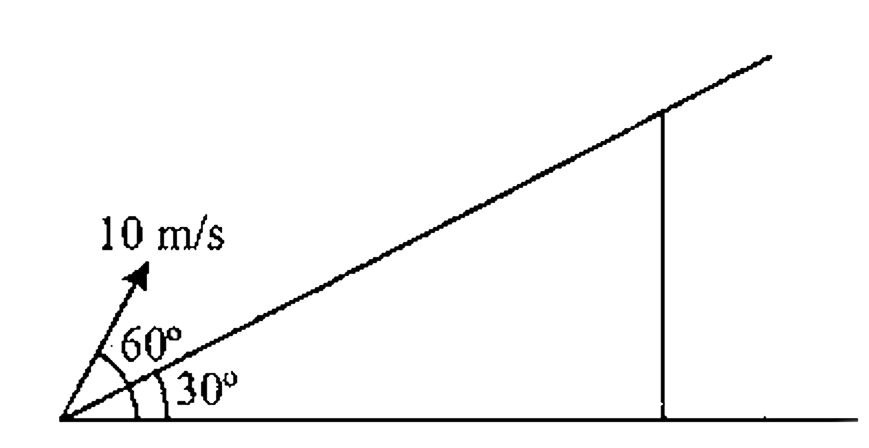 A2√3 secB1√3 secC√3 secD12√3 sec
A2√3 secB1√3 secC√3 secD12√3 seca particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
A21dmB2.1dmC30dmD6dm
A magnetic needle is free to rotate in a vertical plane which makes an angle of 60∘ with the magnetic meridian. If the needle stays in a direction making an angle of tan−1(2/√3) with the horizontal, what would be the true dip at that place?
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View SolutionAn inclined plane makes an angle of 60∘ with horizontal. A disc rolling acceleration equal to:
View SolutionA force of 5N acts on a particle along a direction making an angle of 60∘ with vertical. Its vertical component is
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is

View Solution
