Find the electric field potentail and strength at the centre of a hemisphere fo raidus R ahcged uniformly with the the surface density σ.
To find the electric potential and electric field strength at the center of a uniformly charged hemisphere with radius R and surface charge density σ, we can follow these steps:
Step 1: Understand the Geometry
Consider a hemisphere of radius R charged uniformly with surface charge density σ. The center of the hemisphere is the point where we want to find the electric potential and electric field.
Step 2: Define a Ring Element
To calculate the electric potential, we can consider a differential ring element at an angle θ from the vertical axis. The radius of this ring is rsinθ and its thickness is Rdθ.
Step 3: Calculate Charge of the Ring Element
The area A of the ring can be expressed as:
A=2π(Rsinθ)(Rdθ)=2πR2sinθdθ
The charge dq on this ring is given by:
dq=σ⋅A=σ⋅2πR2sinθdθ
Step 4: Calculate Electric Potential Contribution
The electric potential dV at the center due to this ring is given by:
dV=kdqR=kσ⋅2πR2sinθdθR
This simplifies to:
dV=2πkσRsinθdθ1
Step 5: Integrate to Find Total Potential
To find the total potential V, integrate dV from θ=0 to θ=π2:
V=∫π202πkσRsinθ1dθ
The integral of sinθ is −cosθ, so:
V=2πkσR(−cosθ)π20=2πkσR(0−(−1))=2πkσR
Substituting k=14πϵ0:
V=σR2ϵ0
Step 6: Calculate Electric Field Contribution
Next, we calculate the electric field dE at the center due to the same ring. The vertical component of the electric field dE from the ring is given by:
dE=kdq⋅cosθR2
Substituting dq:
dE=k⋅σ⋅2πR2sinθdθ⋅cosθR2=kσ⋅2πsinθcosθdθ
Using the identity 2sinθcosθ=sin(2θ):
dE=σ4πϵ0sin(2θ)dθ
Step 7: Integrate to Find Total Electric Field
Integrate dE from θ=0 to θ=π2:
E=∫π20σ4πϵ0sin(2θ)dθ
The integral of sin(2θ) is −12cos(2θ):
E=σ4πϵ0(−12cos(2θ))π20=σ4πϵ0(−12(0−1))=σ8πϵ0
Final Results
- The electric potential V at the center of the hemisphere is:
V=σR2ϵ0
- The electric field strength E at the center of the hemisphere is:
E=σ4ϵ0
Consider a hemisphere of radius R charged uniformly with surface charge density σ. The center of the hemisphere is the point where we want to find the electric potential and electric field.
To calculate the electric potential, we can consider a differential ring element at an angle θ from the vertical axis. The radius of this ring is rsinθ and its thickness is Rdθ.
The area A of the ring can be expressed as:
A=2π(Rsinθ)(Rdθ)=2πR2sinθdθ
The charge dq on this ring is given by:
dq=σ⋅A=σ⋅2πR2sinθdθ
The electric potential dV at the center due to this ring is given by:
dV=kdqR=kσ⋅2πR2sinθdθR
This simplifies to:
dV=2πkσRsinθdθ1
To find the total potential V, integrate dV from θ=0 to θ=π2:
V=∫π202πkσRsinθ1dθ
The integral of sinθ is −cosθ, so:
V=2πkσR(−cosθ)π20=2πkσR(0−(−1))=2πkσR
Substituting k=14πϵ0:
V=σR2ϵ0
Next, we calculate the electric field dE at the center due to the same ring. The vertical component of the electric field dE from the ring is given by:
dE=kdq⋅cosθR2
Substituting dq:
dE=k⋅σ⋅2πR2sinθdθ⋅cosθR2=kσ⋅2πsinθcosθdθ
Using the identity 2sinθcosθ=sin(2θ):
dE=σ4πϵ0sin(2θ)dθ
Integrate dE from θ=0 to θ=π2:
E=∫π20σ4πϵ0sin(2θ)dθ
The integral of sin(2θ) is −12cos(2θ):
E=σ4πϵ0(−12cos(2θ))π20=σ4πϵ0(−12(0−1))=σ8πϵ0
- The electric potential V at the center of the hemisphere is:
V=σR2ϵ0
- The electric field strength E at the center of the hemisphere is:
E=σ4ϵ0
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.4
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Find the electric field potential and strength at the center of a hemisphere of radius R charged uniformly with the the surface density σ.
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
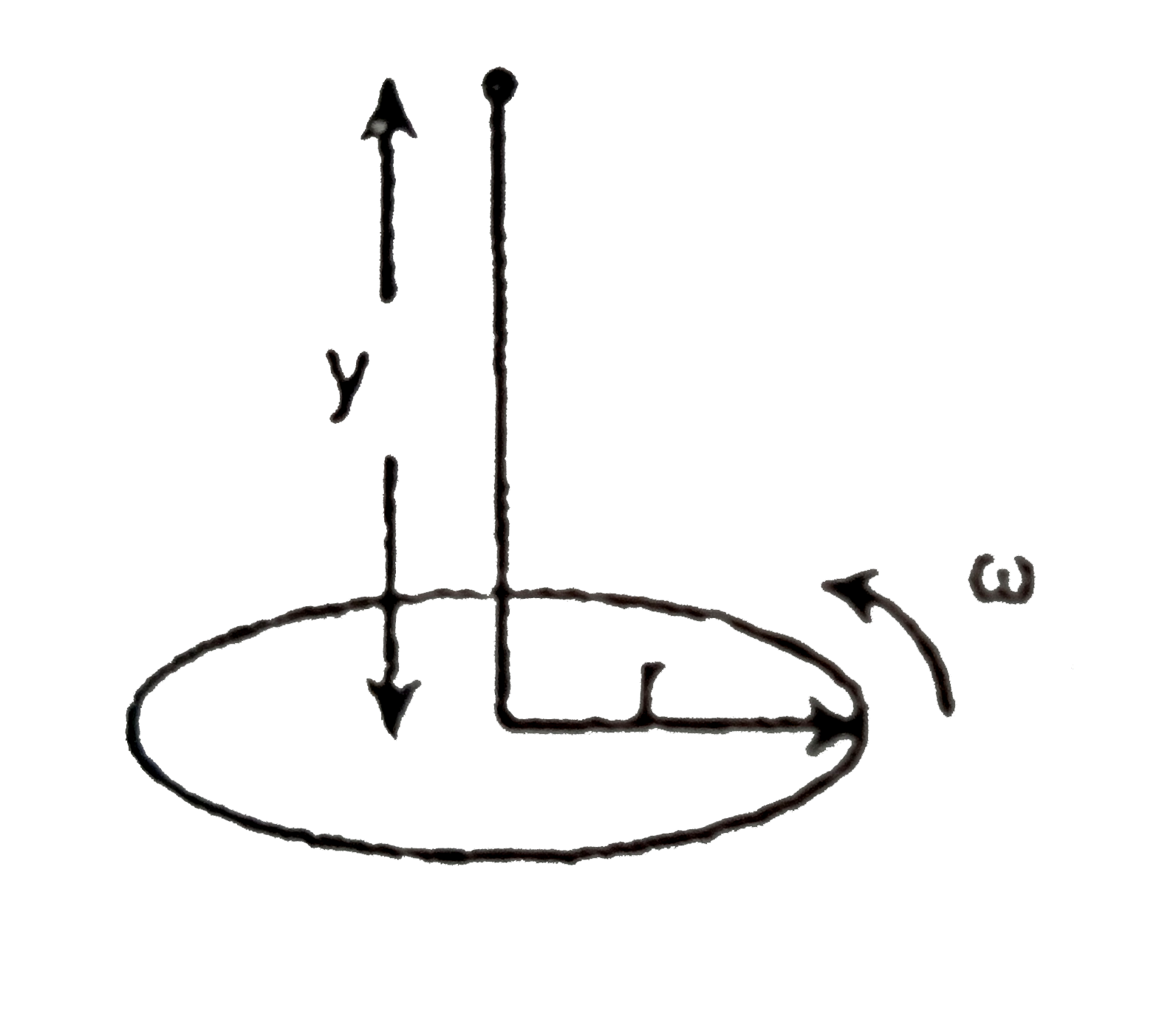
View SolutionCalculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density σ, If the disc spins with angular velocity ω ?
View SolutionA total charge of 5μC is distributed uniformly on the surface of the thin walled semispherical cup. If the electric field strength at the centre of the hemisphere is 9×108NC−1, then the radius of the cup is
(14πε0=9×109N−m2C−2)
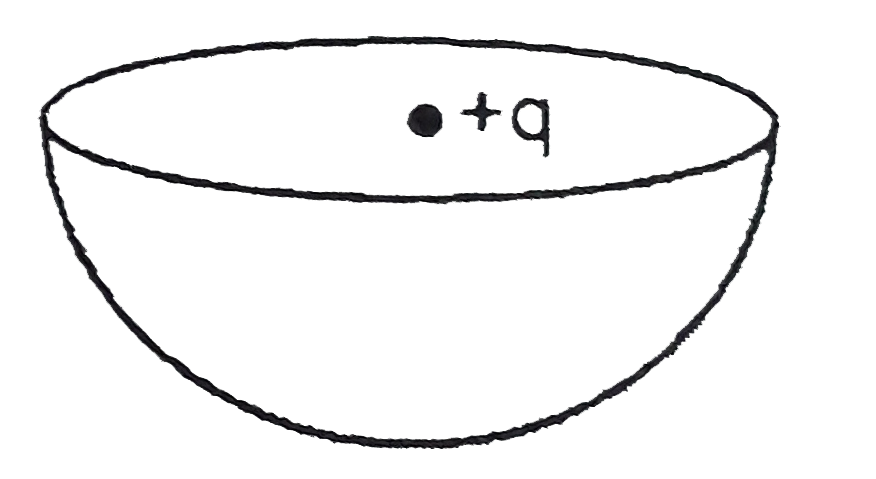
View SolutionA point charge +q is placed at the centre of curvature of a hemisphere. Find flux through the hemispherical surface.
View SolutionA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
View SolutionFind out the flux through the curved surface of a hemisphere of radius R if it is placed in a uniform electric field E as shown in figure
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
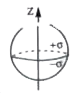
View SolutionA hollow insulating spherical shell has a surfac charge distribution placed upon it, such that the upper hemisphere has a uniform surface charge density σ. While the lower hemisphere has a uniform surface charge density −σ.as shown in the figure. Their interface lies in x-y plane which
View Solution
