Find the equivalent resistance between the point a and b of the circuit shown in figure
Text Solution
Suppose a current i enters the circuit at the point a, a part i1 goes through the 10Ω resistor and the rest I−i1 throught he 5Ω resistor. By symmerty, the current i coming out from the point b will be composed of a part i1 from the 10Ω resistor and i−i1 from the 5Ω (figure) resistor. Applying Kirchhoff a junction law, we can find the current through the middle 5Ω resistor. The current distribution is shown in figure.
We have
Va−Vb=(Va−Vc)+(Vc−Vb)
=(10Ω)ii+(5Ω)(i−i1)
=(5Ω)i+(5Ω)i1. .... (i)
Also, Va−Vb=(Va−Vc)+(Vc−Vd)+(Vd−Vb)
=(10Ω)i1+(30Ω)i1 ...(ii)
Multiplying (i) by 6 and subtracting (ii) from it, we eliminate i1 and get,
5(Va−Vb)=(35Ω)i
or, Va−Vbi=7Ω.
Thus the equivalent resistance between the points aandb is 7Ω.
|
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - worked out Example
1 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Short Answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Exercises
84 Videos
- DISPERSION AND SPECTRABOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
Similar Questions
Knowledge Check
Find the equivalent resistance between the point a and b of the network shown in figure.
 A3B2C1D5
A3B2C1D5The equivalent resistance between the points A and B in A the circuit shown in Fig. is
 A3.12ΩB1.56ΩC6.24ΩD12.48Ω
A3.12ΩB1.56ΩC6.24ΩD12.48ΩThe equivalent resistance between point x and y, of the circuit as shown in the figure is
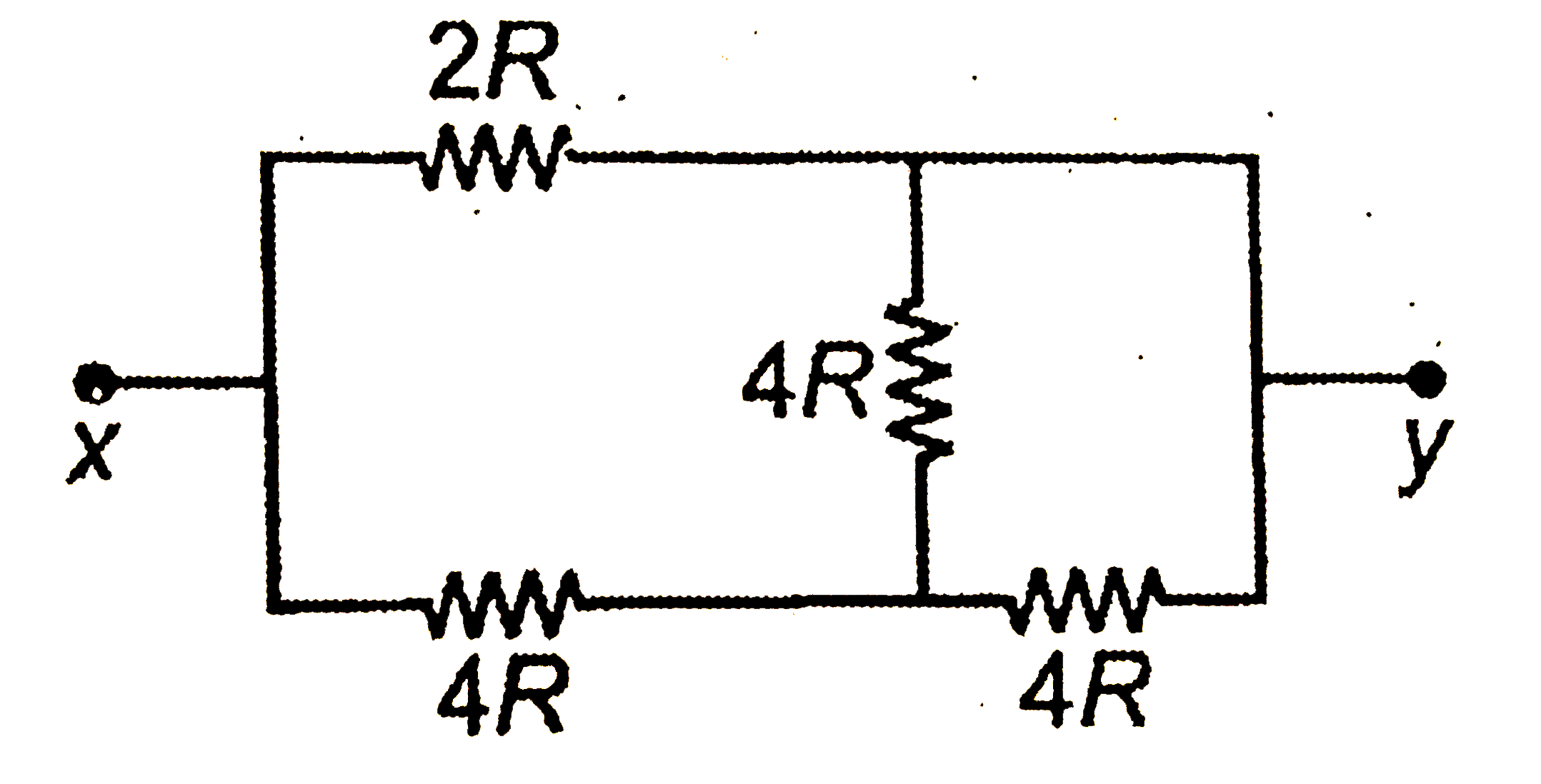 ARB3R2C3R4D8R5
ARB3R2C3R4D8R5
The equivalent resistance between point A and B in the circuit shown in figure is
_PHY_E05_041_Q01.png)
View SolutionFind equivalent resistance between points A and B in the circuit shown.
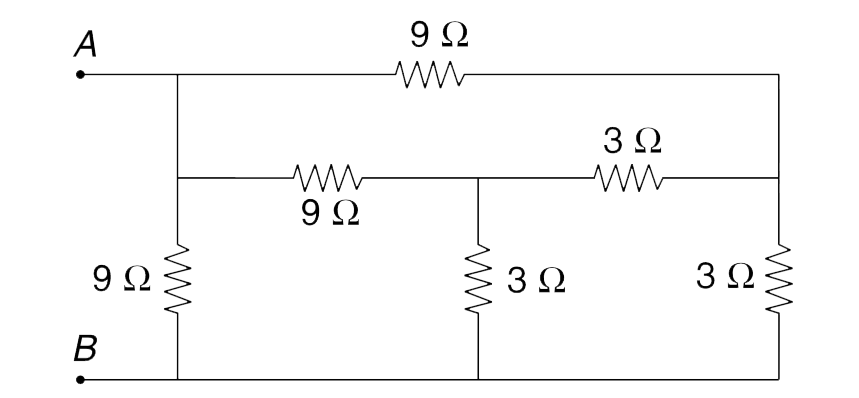
View SolutionFind the equivalent resistance between point a and b in the network shown in figure.
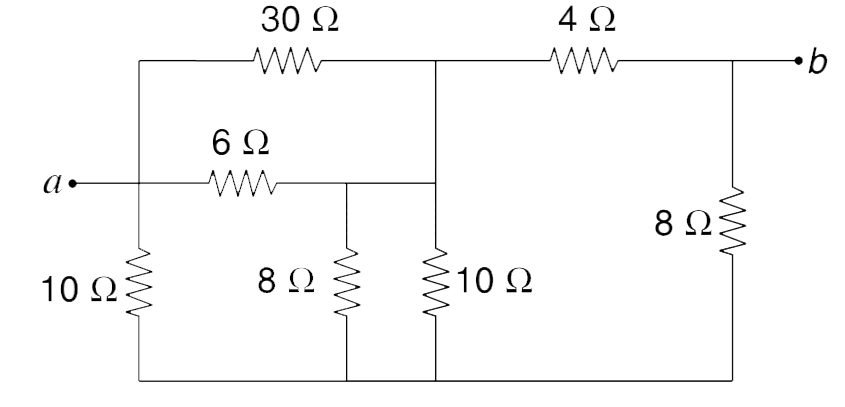
View SolutionCalculate the equivalent resistance between the points A and B in the circuit shown in Fig. (a)
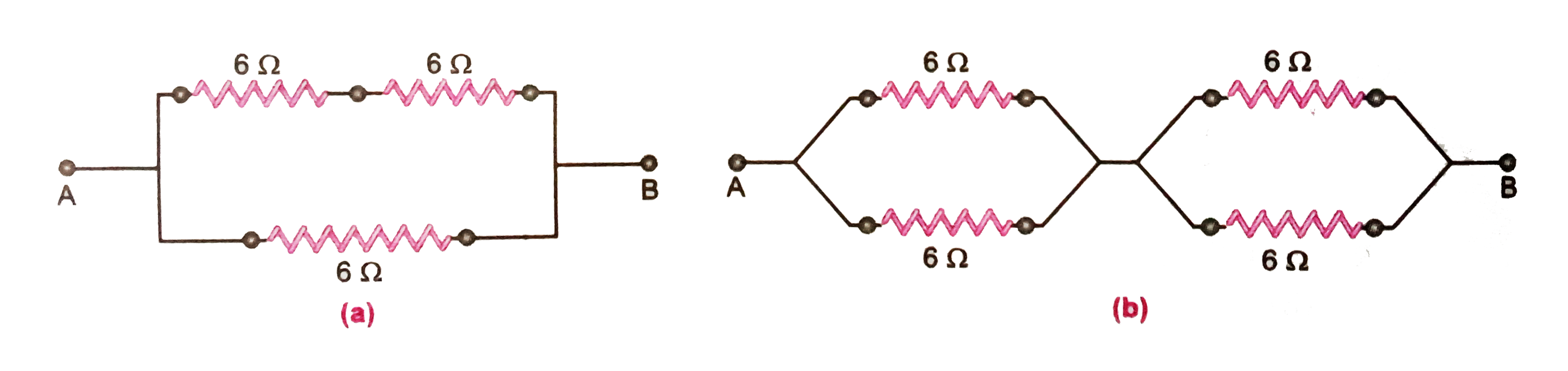
View SolutionThe equivalent resistance between A and B for . the circuit shown in this figure is

View Solution

_PHY_E05_095_Q01.png)