Find the fundamental note emitted by a string of length 10√10 cm under tension of 3.14 kg. Radius of string is 0.55 mm and density =9.8gcm−3.
Step by step video solution for Find the fundamental note emitted by a string of length 10sqrt(10) cm under tension of 3.14 kg. Radius of string is 0.55 mm and density =9.8gcm^(-3). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Find the fundamental note emitted by a string of length 10√10 cm under tension of 3.14 kg. Radius of string is 0.55 mm and density =9.8gcm−3.
View SolutionWhat will be the fundamental note emitted by a string of length 20√10 cm under a tension of 6.28 kg st if its radius and density are 0.2 mm and 19.6 g/cm3, respectively ?
View Solution
Knowledge Check
- Question 1 - Select One
In order to double the frequnecy of the fundamental note emitted by a stratched string the length is reduced to 34 th of the original length and the tension is changed. The factor by which the tension is to be changed is
A38B23C89D94 - Question 2 - Select One
In order to double the frequency of the fundamental note emitted by a stretched string, the length is reduced to 34th of the original length and the tension is changed. The factor by which the tension is to be changed is
A3/8B2/3C8/9D9/4 - Question 3 - Select One
A sphere of radius 25 cm and mass 1 kg is hung by a string of negligible mass and length 40 cm, then tension in the string is -
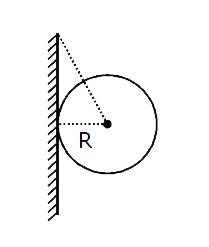 A10.81 NB18.4 NC10 ND8 N
A10.81 NB18.4 NC10 ND8 N
the frequency of a note emitted by a silver wire of length 25 cm is 256 when the tension is 10 kg.Calculate the radius of the wire (Density of silver =10.5×103kgm−3)
View SolutionCalculate the fundamental frequency of a sonometer wire fo length 20cm, tension 25N, cross sectional area 10−2cm2 and density of material =104kg/m3.
View SolutionThe frequency of the note emitted by a silver wire 1 mm in diameter and 50 cm in length is 256 Hz.Find the tension in the wire, if density of silver is 10.5 g cm−3.
View SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x = 0 and the other is at x=l. When string vibrates in fundamental mode, amplitude of the midpoint O of the string is a, tension in a, tension in the string is T and amplitude of vibration is A. Find the total oscillation energy stored in the string.
View SolutionTwo identical charged spheres are suspended by strings of equal lengths. The strings make an angle of 30∘ with each other. When suspended in a liquid of density 0.8gcm−3, the angle remains the same. If density of the material of the sphere is 1.6gcm−3, the dielectric constant of the liquid is
View Solution

