Find the maximum kinetic enegry of photoelectrons liberated form the surface of lithium by electromagnetic radiation whose electric component varies with time as E=a(1+cosωt)cosω0t, where a is a constant, ω=6.0.1014s−1 and ω0=360.1015s−1.
We write
E=a(1+cosωt)cosω0t
=acosω0t+a2[cos(ω0−ω)t+cos(ω0+ω)t]
It is abvious that light has there frequencies and the maximum K.E. of photon electrons ejected is
h(ω+ω0)−ALi
where ALi=2.39eV. Substituting we get 0.37ev.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise2videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Optics Of Moving Sources22videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems92videos
MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
Similar Questions
The surface of a metal of work funcation ϕt is illumicated by light whose electric field component varies with time as E=E0[1+cosωt]sinω0t. Find the maximum kinetic energy of photonelectrons emitted from the surface.
View SolutionFind the mean radiation power of an electorn performing harmonic oscillations with amplitude a=0.10nm and frequency ω=6.5.1014s−1
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle moves in xy plane according to the law x = a sin ωtand y = a(1 – cosωt) where a and ω are constants. The particle traces
Aa parabolaBa straight line equallyinclined to x and y axesCa circleDa distance proportional to time - Question 2 - Select One
A particle of mass m and charfe Q is placed in an electric filed W which varies with time t as E = E0sinωt. It will undergo simple harmonic motion of amplitude.
AQE20mω2BQE0mω2C√QE0mω2DQE0mω - Question 3 - Select One
What is the percentage hydrolysis of NaCN is N/80 soluiton, when the dissociation constant for HCN is 1.3×10−9 and Kw=1.0×10−14
A2.48B5.26C8.2D9.6
What will be the maximum kinetic energy of the photoelectrons ejected from magnesium (for which the work -function W=3.7 eV) when irradiated by ultraviolet light of frequency 1.5×1015s−1.
View SolutionFind how the voltage across the capacitor C varies with time t after closing of the switch Sw at the moment t=0.
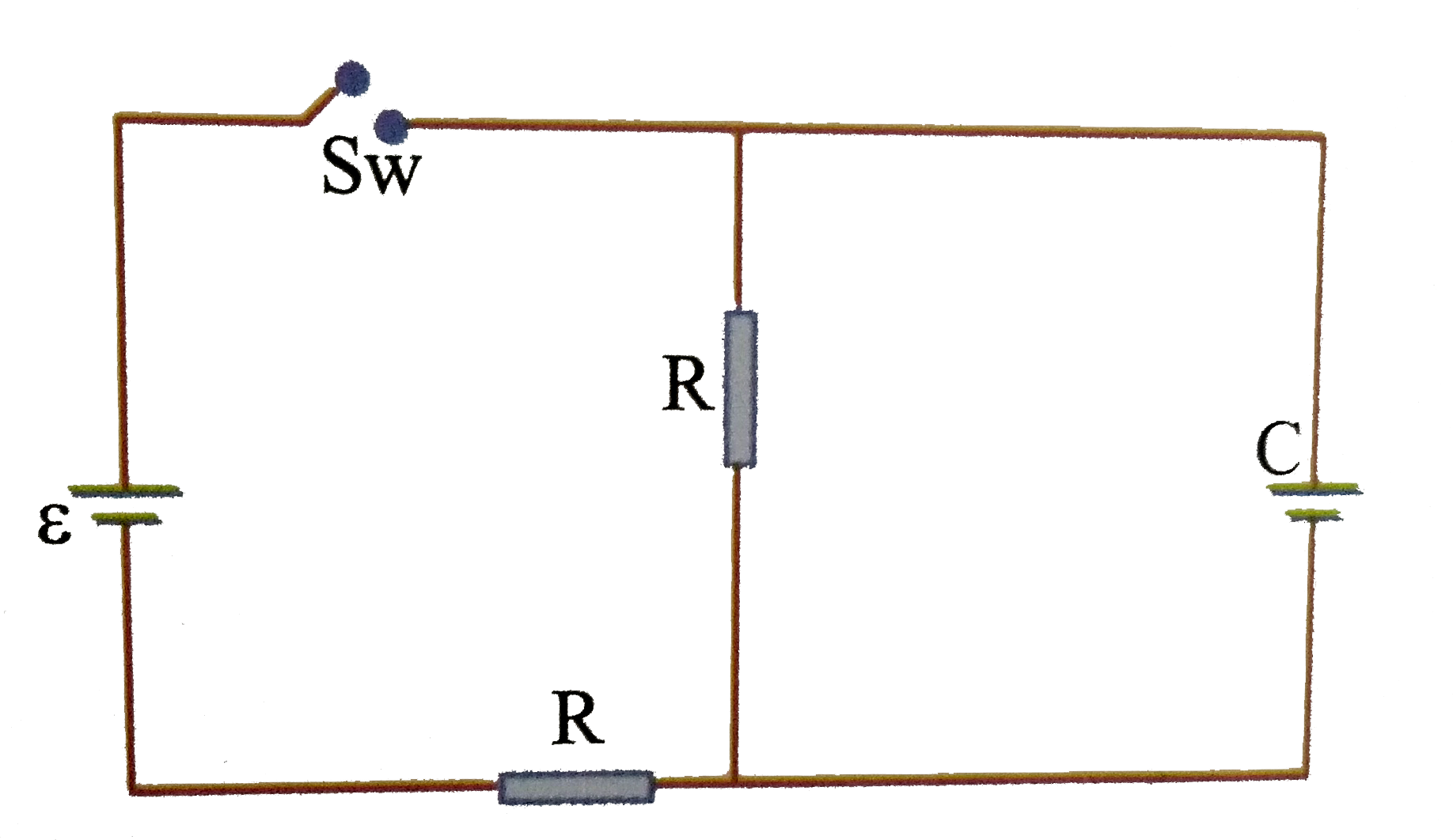 .View Solution
.View SolutionA charged particle moves along the y axis according to the law y=acosωt, and the point of observation P is located on the x axis at a distance l from the particle (l>>a). Find the ratio of electromagnetic radiation flow densities S1/S2 at the point P at the moments when the corrdinate of the particle y1=0 and y2=a. Calculate that ratio if ω=3.3.106s−1 and l=190m.
View SolutionElectromagnetic radiation whose electric component varies sinusoidally with time as E=C1(C2+C3cosωt)cosω0t,whereC1,C2andC3 are constants in incident on lithium and liberates photoelectrons. If the kinetic energy of the most energetic photoelectrons be 0.592×10−19J find the work function of lithium given that ω0=3.6×1015 rad/sec and ω=6×1014 rad/sec.
View SolutionAn electromagnetic radiation whose electric component varies with time as E=E0(1+cosωt)cosω0t(ω=6×1015rad/s,ω0=2.8×1014rad/s) is incident on a lithium surface (work function =2.39 eV) .
The maximum kinetic energy of a photoelectron liberated from the lithium surface is (h=4.14 xx10^(-15) eV-s)View Solution

