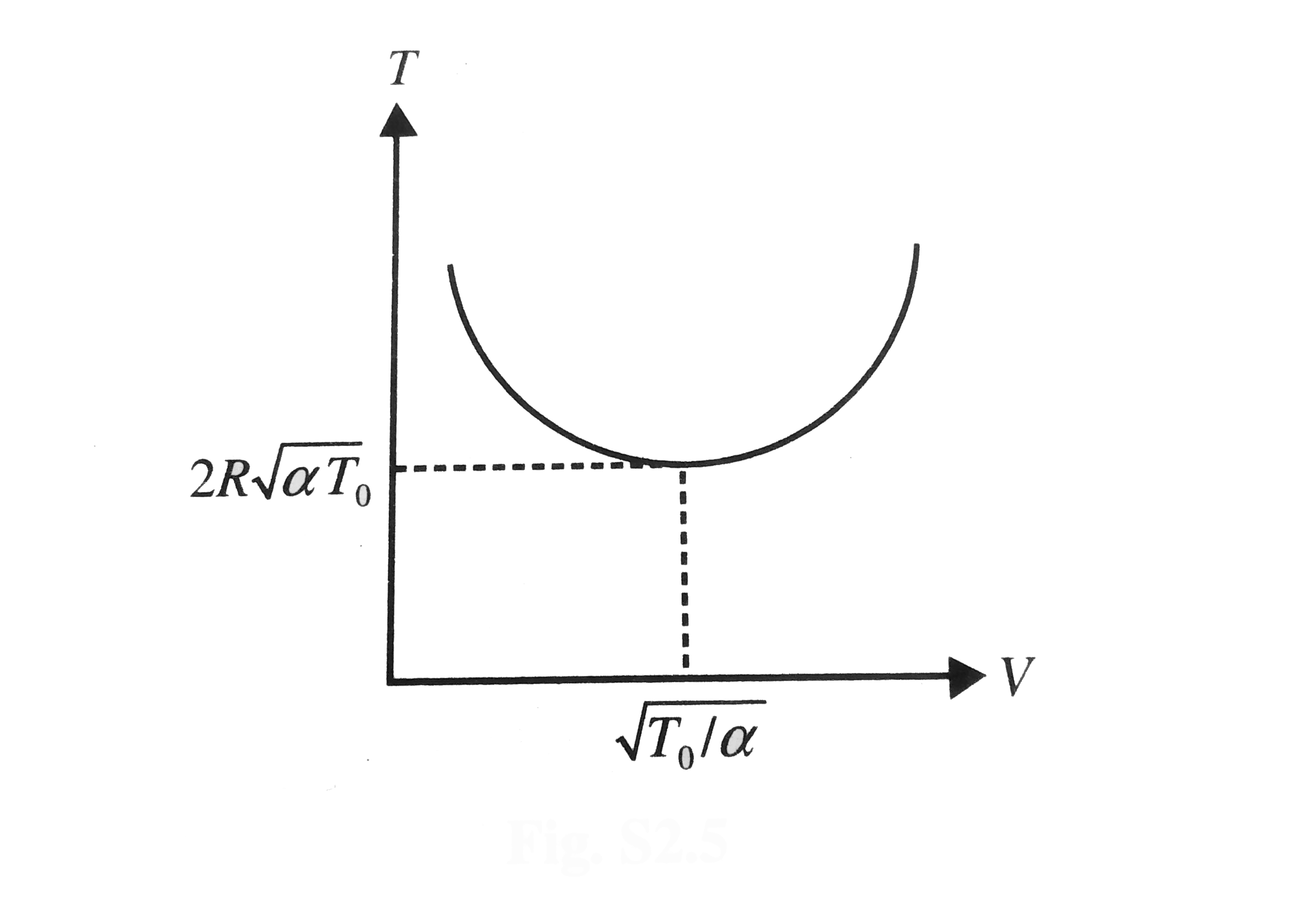
Find the minimum attainable pressure of an ideal gas in the process $T = T_{0} + α V^{2}$ , Where $T_{0}$ and $α$ are positive constant and $V$ is the volume of one mole of gas. Draw the approximate $T - V$ plot of this process.

Video Solution

Text Solution

Verified by Experts

Given,
$T = T_{0} + α V^{2}$ (i)
For 1 mol of a gas, $P V = R T$
or $V = \frac{R T}{P}$
Substituting this value in Eq. (i) we get
$T = T_{0} + α {(\frac{R T}{P})}^{2} = T_{0} + α \frac{R^{2} T^{2}}{P^{2}}$
or $T P^{2} = T_{0} P^{2} + α R^{2} T^{2}$
or $P = \sqrt{α} R T {(T - T_{0})}_{0}^{- 1 / 2}$
After differenating, we get
$\frac{d P}{d T} = \sqrt{α} R [{(T - T_{0})}_{0}^{- 1 / 2} \frac{1}{2} T {(T - T_{0})}_{0}^{- 3 / 2}]$
For minimum pressure,
$\frac{d P}{d T} = 0$
$∴ 0 = \sqrt{α} R [{(T - T_{0})}_{0}^{- 1 / 2} \frac{1}{2} T {(T - T_{0})}_{0}^{- 3 / 2}]$
After solving, $T = 2 T_{0}$
Form Eq. (ii),
$P_{min} = \sqrt{α} R 2 T_{0} {(2 T_{0} - T_{0})}_{0}^{- 3 / 2}$
$= 2 R \sqrt{α T_{0}}$

Updated on:21/07/2023