Find the minimum force required to drag a hard polythene plate of area 2m2 on a thin film of oil of thickness 0.25cm and η=15 poise. Assume the speed of the plate is 10cms−1.
To find the minimum force required to drag a hard polythene plate on a thin film of oil, we can use the formula for viscous force:
F=μ⋅A⋅vh
where:
- F is the force,
- μ is the viscosity of the fluid,
- A is the area of the plate,
- v is the velocity of the plate,
- h is the thickness of the fluid layer.
1. Identify the given values:
- Viscosity (μ) = 15 poise
- Area (A) = 2 m² = 2×104 cm² (since 1 m² = 104 cm²)
- Velocity (v) = 10 cm/s
- Thickness (h) = 0.25 cm
2. Convert viscosity to appropriate units:
- 1 poise = 0.1 Pa·s, so:
μ=15 poise=15×0.1 Pa⋅s=1.5 Pa⋅s
3. Substitute the values into the formula:
F=μ⋅A⋅vh
F=15 poise⋅(2×104 cm2)⋅10 cm/s0.25 cm
4. Calculate the force:
- First, calculate vh:
vh=10 cm/s0.25 cm=40 s−1
- Now substitute back into the equation:
F=15⋅(2×104)⋅40
F=15⋅800000=12000000 dyne
5. Convert dyne to Newton (if needed):
- Since 1 Newton=105 dyne:
F=12000000 dyne105=120 N
Final Answer:
The minimum force required to drag the hard polythene plate is 1.2×107 dyne or 120 N.
- F is the force,
- μ is the viscosity of the fluid,
- A is the area of the plate,
- v is the velocity of the plate,
- h is the thickness of the fluid layer.
- Viscosity (μ) = 15 poise
- Area (A) = 2 m² = 2×104 cm² (since 1 m² = 104 cm²)
- Velocity (v) = 10 cm/s
- Thickness (h) = 0.25 cm
- 1 poise = 0.1 Pa·s, so:
μ=15 poise=15×0.1 Pa⋅s=1.5 Pa⋅s
F=μ⋅A⋅vh
F=15 poise⋅(2×104 cm2)⋅10 cm/s0.25 cm
- First, calculate vh:
vh=10 cm/s0.25 cm=40 s−1
- Now substitute back into the equation:
F=15⋅(2×104)⋅40
F=15⋅800000=12000000 dyne
- Since 1 Newton=105 dyne:
F=12000000 dyne105=120 N
The minimum force required to drag the hard polythene plate is 1.2×107 dyne or 120 N.
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.3
9 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Subjective
16 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
Calculate the force required to separate the glass plates of area 10−2m2 with a film of water 0.05 mm thickness between them (surface tension of water =70×10−3N/m))
View SolutionA plate has a length (5±0.1) cm and breadth (2±0.01) cm . Then the area of the plate is
View Solution
A space 2.5cm wide between two large plane surfaces is filled with oil. Force required to drag a very thin plate of area 0.5m2 just midway the surfaces at a speed of 0.5msec is 1N. The coefficient of viscosity in kg−sm2 is:
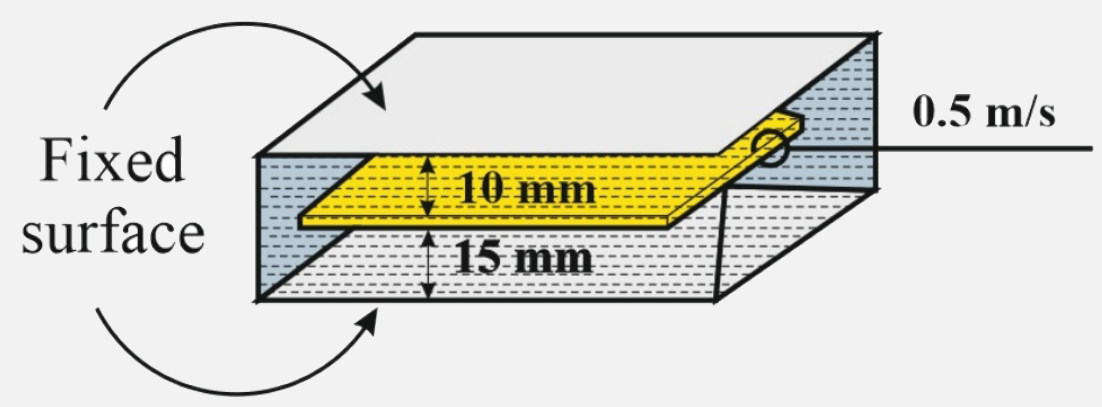
View SolutionGlycerine is filled in 25 mm wide space between two large plane horizontal surfaces. A thin plate of area 0.75m2 at a distance of 10 mm from one of the surfaces is in a horizontal position be the plates inside the glycerine. It is dragged horizontally at a constant speed of 0.5ms2. Take coefficient of viscosity η= 0.5 Ns m−2. What is the force required to drag the plate at a constant speed (in newton) ?
View SolutionFind the area of the cardboard required to make a closed box of length 25cm, 0.5m and height 15cm.
View SolutionThe space between two large plane surfaces is 2.5 cm and it is filled with glycerine.
What force is required to drag a very thin plate 1m2 in area, between the surfaces at a speed of 1m/s ? (The plate is at a distance of 1 cm from one of the surfaces. ) (η=0.75Ns/m2)
View SolutionThe length and breadth of a plate are (6±0.1)cmand(4±0.2)cm respectively. The area of the plate is
View SolutionA circular plate of area 0.4cm2 is kept at distance of 2m source of power πW. Find the amount of energy received by plate in 5 secs.
View SolutionBetween a plate of area 100cm2 and another plate of area 100m2 there is a 1mm, thick layer of water, if the coefficient of viscosity of water is 0.01 poise, then the force required to move the smaller plate with a velocity 10cms−1 with reference to large plate is
View SolutionAflat plate of area 0.05m2 is separated from another large plate at rost by a liquid layer of uniform thickness 1μm. The tangential force needed to move the smaller plate with a constant velocity of 10cms−1 i s 20 N. Calculate the coefficent of viscosity of the liquid.
View Solution
