Find the moment of inertia of a circular disk or solid cylinder of radius R about the axis through the centre and perpendicular to the flat surface.
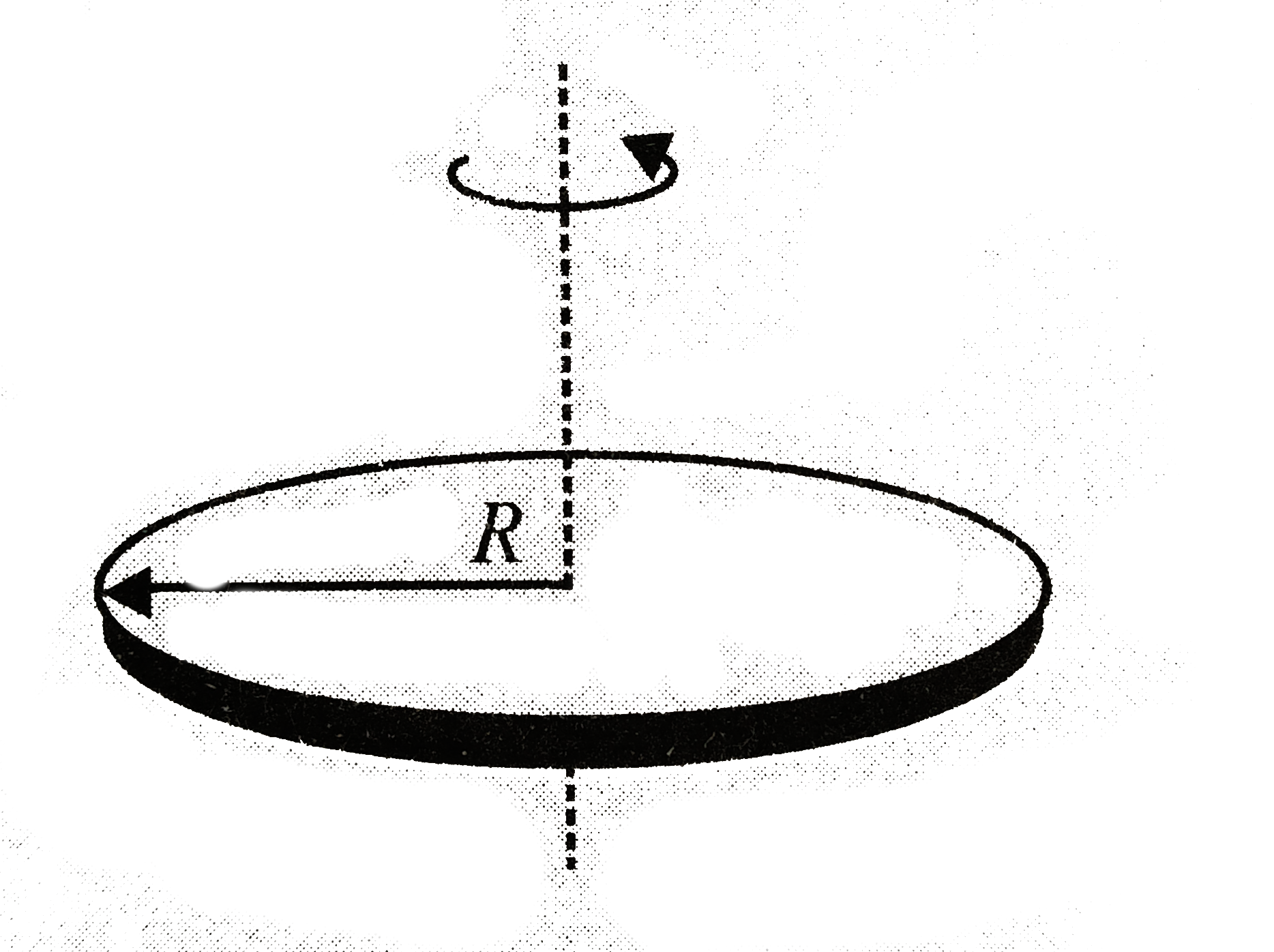
The figure shows that the appropriate mass element is a circular ring of radius r and width dr.
Its area is dA=2πrdr and its mass is dm=σdA.

where σ=MA is the real mass density. The moment of inertia of this element is
dI=dmr2=2πar3dr
For the whole body.
I=2πσ∫R0r3dr=12πσR4
The mass of whole disck or cylinder is
M=σA=σsπR2, and so I=12MR2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionFind the moment of inertia of a cylinder of mass M, radius R and length L about an axis passing through its centre and perpendicular to its symmetry axis. Do this by integrating an elemental disc along the length of the cylinder.
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionFind the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to plate is
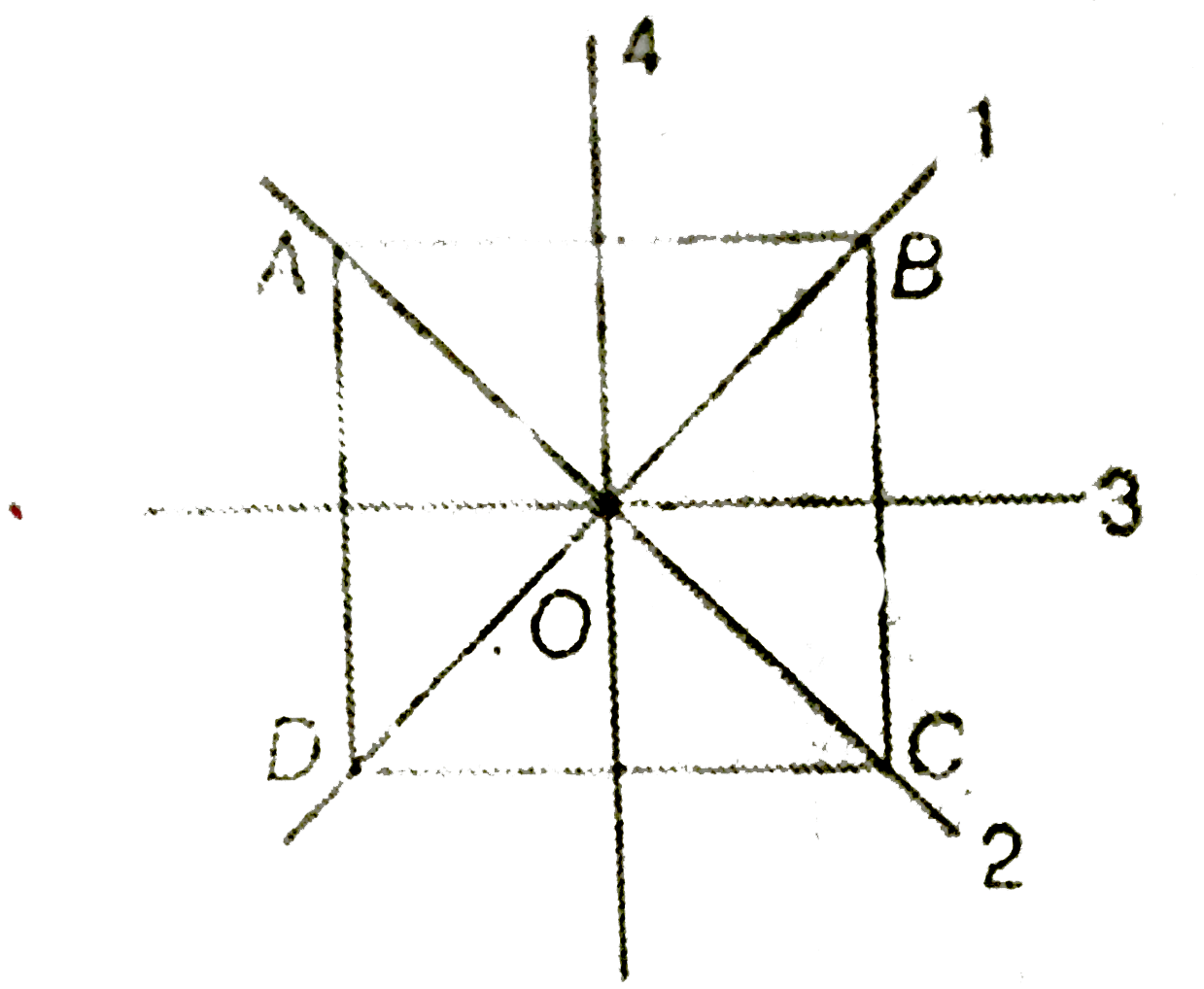
View Solution
