Find the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
To find the moment of inertia of a uniform cylinder about an axis through its center of mass and perpendicular to its base, we can follow these steps:
1. Understand the Geometry:
- We have a uniform cylinder with mass M and radius R. The axis of rotation is through its center and perpendicular to its base.
2. Use the Definition of Moment of Inertia:
- The moment of inertia I is defined as:
I=∫r2dm
where r is the distance from the axis of rotation to the mass element dm.
3. Consider the Cylinder as Disks:
- We can think of the cylinder as being made up of many thin disks stacked on top of each other. Each disk has a thickness dz and radius R.
4. Find the Mass Element:
- The mass of a thin disk can be expressed as:
dm=ρdV
where ρ is the density of the cylinder and dV is the volume of the disk.
5. Calculate the Volume of a Thin Disk:
- The volume of a thin disk of thickness dz is:
dV=πR2dz
Therefore, the mass element becomes:
dm=ρπR2dz
6. Substitute into the Moment of Inertia Formula:
- The distance r from the axis of rotation to the mass element for each disk is R. Thus, we have:
I=∫R2dm=∫R2ρπR2dz
7. Integrate Over the Height of the Cylinder:
- If the height of the cylinder is h, the limits of integration for z will be from 0 to h:
I=R2ρπR2∫h0dz=R2ρπR2h
8. Express Density in Terms of Mass:
- The density ρ can be expressed as:
ρ=MπR2h
where M is the total mass of the cylinder.
9. Substitute Density Back into the Moment of Inertia:
- Substituting ρ into the moment of inertia expression gives:
I=R2(MπR2h)πR2h=12MR2
10. Final Result:
- Therefore, the moment of inertia of the uniform cylinder about the specified axis is:
I=12MR2
- We have a uniform cylinder with mass M and radius R. The axis of rotation is through its center and perpendicular to its base.
- The moment of inertia I is defined as:
I=∫r2dm
where r is the distance from the axis of rotation to the mass element dm.
- We can think of the cylinder as being made up of many thin disks stacked on top of each other. Each disk has a thickness dz and radius R.
- The mass of a thin disk can be expressed as:
dm=ρdV
where ρ is the density of the cylinder and dV is the volume of the disk.
- The volume of a thin disk of thickness dz is:
dV=πR2dz
Therefore, the mass element becomes:
dm=ρπR2dz
- The distance r from the axis of rotation to the mass element for each disk is R. Thus, we have:
I=∫R2dm=∫R2ρπR2dz
- If the height of the cylinder is h, the limits of integration for z will be from 0 to h:
I=R2ρπR2∫h0dz=R2ρπR2h
- The density ρ can be expressed as:
ρ=MπR2h
where M is the total mass of the cylinder.
- Substituting ρ into the moment of inertia expression gives:
I=R2(MπR2h)πR2h=12MR2
- Therefore, the moment of inertia of the uniform cylinder about the specified axis is:
I=12MR2
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
The moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionFind the moment of inertia of a half uniform ring (mass m, radius r) about its center.
View Solution
Knowledge Check
A uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
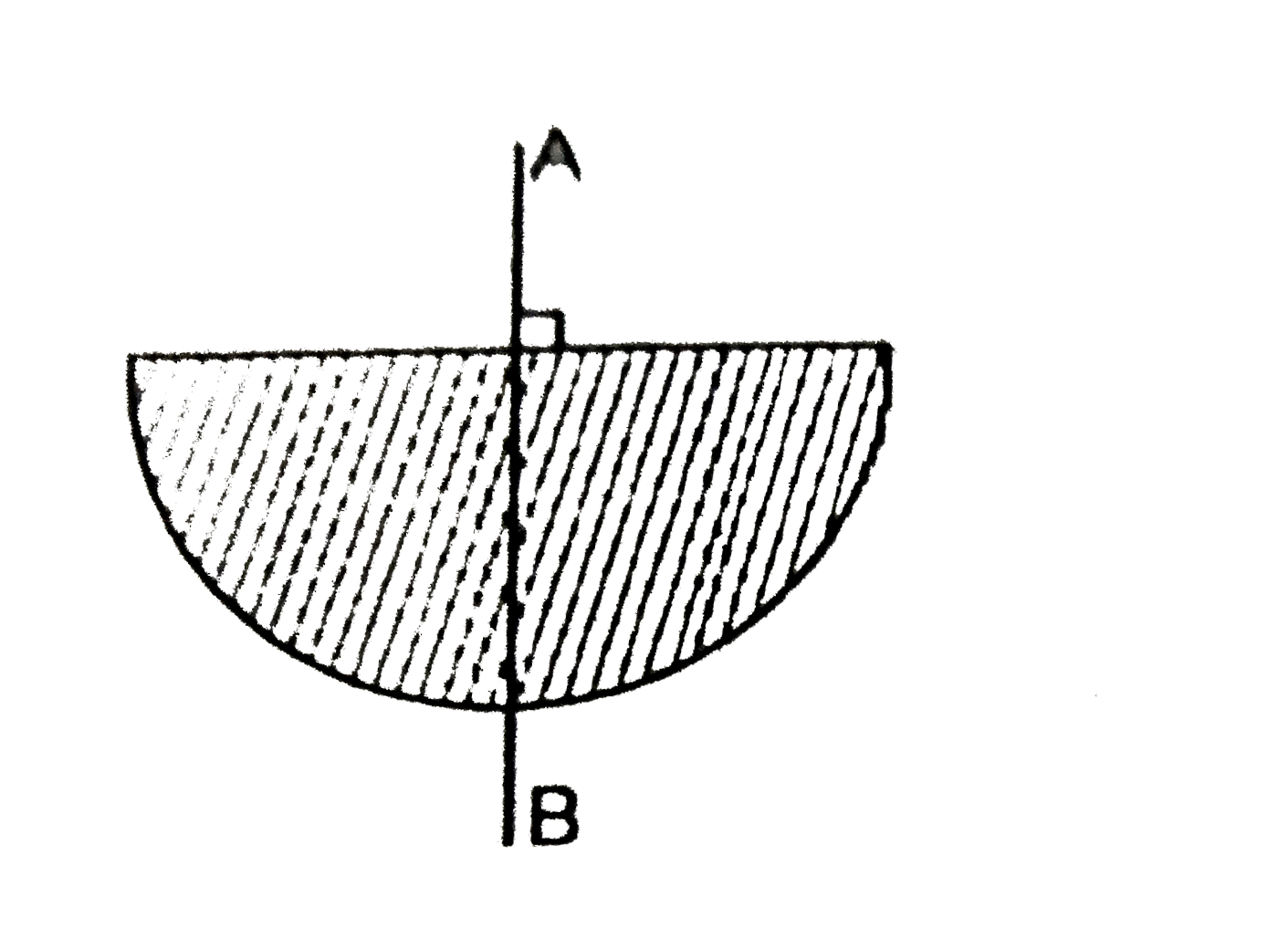 AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2
AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
AMR22−M(4R3π)2BMR22−M(√24R3π)2CMR22+M(4R3π)2DMR22+M(√24R3π)2The radius of gyration of an uniform rod of length L about an axis passing through its centre of mass and perpendicular to its length is.
AL√2BL2√12CL√3DL√2
The moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionThe moment of inertia of a uniform semicircular wire of mass M and radius R about an axis passing through its centre of mass and perpendicular to its plane is xMR210. Find the value of x? (Take π2=10)
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2 R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I, and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2 then
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View Solution
