Find the poistions of the principle planes, the focal length and the sign of the optical power of a thick convex-concave glass lens
(a) whose thickness is equal to d and curvature radii of the surfaces are the same and equal to R,
(b) whose refractive surfaces are concentric and have the curvarure radii R1 and R2(R2>R1).
The power of the lens is (as in the pervious problem)
Φ=n−1R−n−1R−dn(n−1R)(−n−1R)=d(n−1)2nR2>0.
The principle planes are located on the side of the convex surface at a distance d from each other, with the front principle plane being removed from the conve surfcae of the lens by a distance R/(n−1).
(a) Here Φ=−n−1R1+n+1R2+R2−R1n(n−1)2R1R2
=(n−1)(R2−R1)R2R1[−1+n−1n]
=−n−1n(1R1−1R2)<0
Both principle planes pass through the common centre of curvature of the surfcaes of the lens.

Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light
33 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light
60 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
Calculate the positions of the principle planes and focal points of a thick convex-concave glass lens if the curvature radius of the convex surface is equal to R1=10.0cm and of the concave surface to R2=5.0cm and the lens thickness is d=3.0cm.
View SolutionFind the focal length of the lens shown in the figure. The radii of curvature of both the surfaces are equal to R
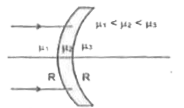
View Solution
Knowledge Check
The capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
A4πε0R2B4πε0(R2−R1)R1R2C4πε0R1R2(R2−R1)D4πε0R1The two spherical surfaces of a double concave lens have the same radius of curvature R, and the refractive index of the medium enclosed by the refracting surfaces is μ then the focal length of the lens is
Af=R2Bf=R2(μ−1)Cf=R2(1−μ)Df=−(μ−1)R2A convex lens has the same radius of curvature (R ) for both the surfaces. For what value of the refractive index of the material of the convex lens, the numerical values of f and R are equal ?
A1.4B1.5C1.55D1.6
Find the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
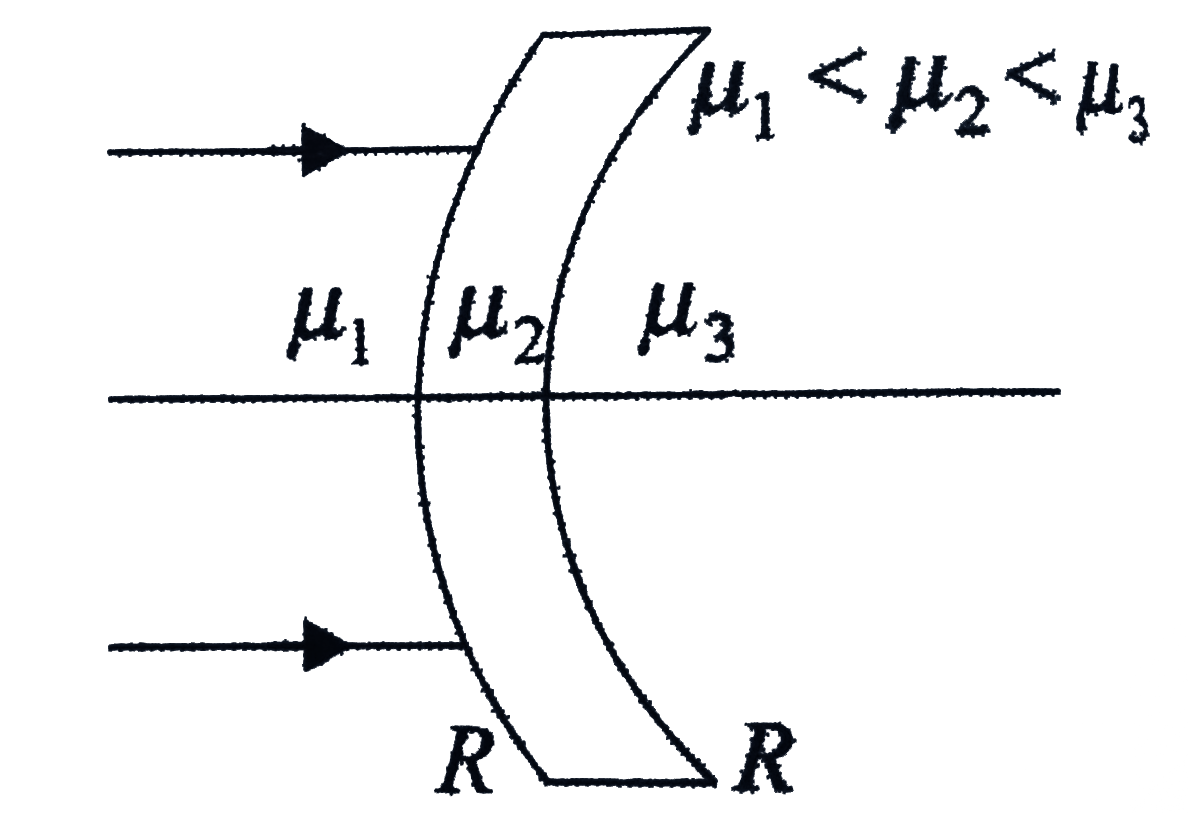
View SolutionDetermine the focal length of a concave spherical mirror which is manufactured in the form of a thin symmetric biconvex glass lens one of whose surfaces is silvered. The curvature radius of the lens surface is R=40cm.
View SolutionFind the radius of curvature of the convex surface of a plano-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionFind the radius of curvature of the convex surface of a plano-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionFind the radius of curvature of the convex surface of a plan-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View Solution
