Find the positions of the perinciple planes, the focal and model points of a thin biconvex symmetric glass lens with curvature radius of its surfaces equal to R=7.50cm. There is air on one side of the lens and water on the other.
The primary and secondary focal length of a thick lens are given as,
f=−(n/Φ){1−(d/n')Φ2}
and f'=+(n''/Φ){1−(d/n')Φ1},
where Φ is the lens power n,n' and n'' are the refractive indices of first medium, lens material and the second medium beyond the lens. Φ1 and Φ2 are the powers of first second spherical surfcae of the lens.
Here, n=1, for lens, n'=n, fro air
and n''=n0, for water.
So, f=−1/Φ1andf'=+n0/Φ}, as d≈0, (1)
Now, power of a thin lens,
Φ=Φ1+Φ2,
where, Φ1=(n−1)R
and Φ2=(n0−n)−R
So, Φ=(2n−n0)/R
From equations (1) and (2), we get (2)
f=−R(2n−n−1)=−11.2cm
and f=n0R(2n−n0−1)=+14.9cm.
Since the distance between the primary principle point and primary nodal point is given as,
x=f{(n''−n)/n''}
So, in this case, x=(n0/Φ)(n0−1)/n0=(n0−1)/Φ
=n0Φ−1Φ=f'+f=3.7cm.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light33videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light60videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems92videos
MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
Similar Questions
Calculate the positions of the principle planes and focal points of a thick convex-concave glass lens if the curvature radius of the convex surface is equal to R1=10.0cm and of the concave surface to R2=5.0cm and the lens thickness is d=3.0cm.
View SolutionCalculate the focal length of a biconvex lens in air if the radii of its surfaces are 60 cm and 15 cm. Refractive index of glass = 1.5
View Solution
Knowledge Check
- Question 1 - Select One
A plano-concave lens is made of glass (R.l. = 1.5) and the radius of curvature of the curved face is 50 cm. The power of the lens is
A-1.0DB-0.5DC+1.0DD+0.5 D - Question 2 - Select One
A plano-convex lens is made of glass of refractive index 1.6. the radius of curvature of its curved surface is 30 cm. What is the focal length of the lens ?
A50 cmB75 cmC100 cmD150 cm
Find the focal length of the lens shown in the figure. The radii of curvature of both the surfaces are equal to R
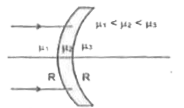 View Solution
View SolutionA point source is located at a distance of 20cm from the front surface of a symmetrical glass biconvex lens. The lens is 5.0cm thick and the curvature radius of its surfaces is 5.0cm. How far beyond the rear surface of this lens is the image of the source fromed ?
View SolutionA system consists of a thin symmetrical converging glass lens with the curvature radius of its surfcaes R=38cm and a plane mirror oriented at right angles to the optical axis of the lens. What is the optical power of this system when the space between the lens and the mirror is filed up with water ?
View SolutionTwo identical thick symmetrical biconvex lenses are put close together. The thickness of each equals the curvature radius of its surfaces, i.e d=R=3.0cm. Find the optical power of this system in air.
View SolutionFind the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
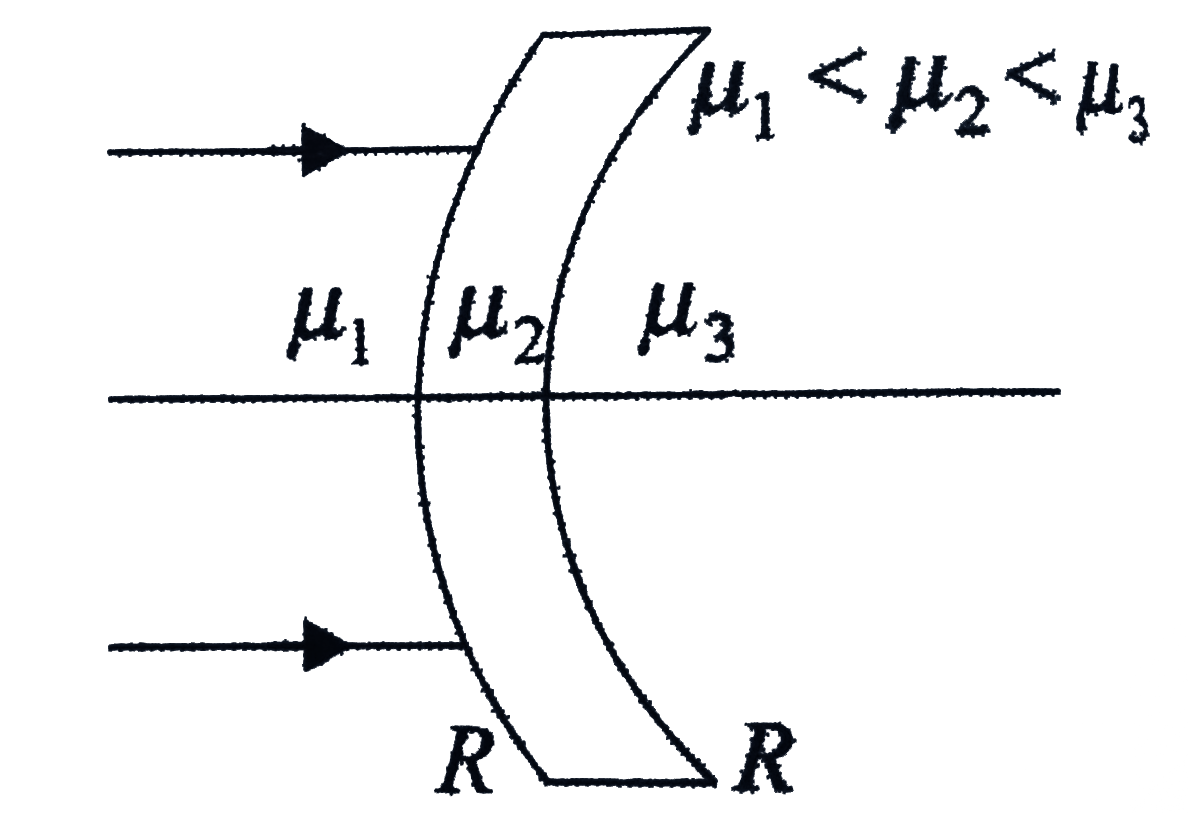 View Solution
View SolutionThe focal length of an equiconvex lens placed in air is equal to radius of curvature of either surface. Is it true ?
View Solution

