Find the stored energy in a capacitor using force between the plates.
To find the stored energy in a capacitor using the force between the plates, we can follow these steps:
1. Define the Capacitor Configuration:
- Consider a parallel plate capacitor with plate area A, plate separation d, and charge q on the plates.
2. Calculate Charge Density:
- The surface charge density σ on the plates is given by:
σ=qA
3. Determine Electric Field:
- The electric field E between the plates of a parallel plate capacitor is given by:
E=σϵ0=qϵ0A
- However, since we are interested in the force, we will consider the electric field due to one plate, which is:
E=σ2ϵ0=q2ϵ0A
4. Calculate the Force on One Plate:
- The force F acting on one plate due to the electric field from the other plate is:
F=qE=q(q2ϵ0A)=q22ϵ0A
5. Work Done by External Force:
- To increase the separation d between the plates, an external force must do work against the attractive force between the plates. The work done W is given by:
W=F⋅d=(q22ϵ0A)d
6. Relate Work Done to Stored Energy:
- The work done on the capacitor is equal to the energy stored in the capacitor. Thus, we can express the energy U stored in the capacitor as:
U=W=q2d2ϵ0A
7. Substitute Capacitance:
- The capacitance C of a parallel plate capacitor is given by:
C=ϵ0Ad
- Rearranging gives d=ϵ0AC. Substituting this into the energy equation:
U=q22C
Final Expression for Stored Energy:
Thus, the stored energy in the capacitor can be expressed as:
U=q22C
- Consider a parallel plate capacitor with plate area A, plate separation d, and charge q on the plates.
- The surface charge density σ on the plates is given by:
σ=qA
- The electric field E between the plates of a parallel plate capacitor is given by:
E=σϵ0=qϵ0A
- However, since we are interested in the force, we will consider the electric field due to one plate, which is:
E=σ2ϵ0=q2ϵ0A
- The force F acting on one plate due to the electric field from the other plate is:
F=qE=q(q2ϵ0A)=q22ϵ0A
- To increase the separation d between the plates, an external force must do work against the attractive force between the plates. The work done W is given by:
W=F⋅d=(q22ϵ0A)d
- The work done on the capacitor is equal to the energy stored in the capacitor. Thus, we can express the energy U stored in the capacitor as:
U=W=q2d2ϵ0A
- The capacitance C of a parallel plate capacitor is given by:
C=ϵ0Ad
- Rearranging gives d=ϵ0AC. Substituting this into the energy equation:
U=q22C
Thus, the stored energy in the capacitor can be expressed as:
U=q22C
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Tough & Tricky PROBLEMS
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Textbook Exercise)
11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 5
18 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Types of capacitors & Energy stored in capacitor| Force between the plates of capacitor
View SolutionA parallel plate capacitor of capacitance C0 is connected across a battery of voltage V. Calculate the change in energy stored in the capacitor if distance between both the plates is decreased to half of its original value.
View Solution
Knowledge Check
Energy can be stored by an LC circuit oscillating at its natural frequency. Energy stored in a capacitor is in form of electric field between the plates. An inductor stores energy in form of magnetic field. If the inductor connected across capacitor, the voltage across the capacitor will drive the current through inductor, building up a magnetic field around it. The voltage across the capacitor falls to zero as the charge is used up by the current flow. Now the energy stored in the coil's magnetic field induces a voltage across the coil, because inductor opposes the current change. Thus energy required to charge the capacitor is extracted from the magnetic field.
We cannot use LC oscillator:to, produce:AVery high frequenciesBVery low.frequenciesCHigh frequenciesDAudio frequenciesFind out total energy stored in the capacitors.
A500μJB300μJC600μJD1300μJ
A parallel plate air filled capacitor having area 40cm2 and plate spacing 1.0 mm is charged to a potential difference of 500V. Find (a) the capacitance, (b) the magnitude of the charge on each plate ( c) the stored energy, (d) the electric field between the plates and (e ) the energy density between the plates.
View SolutionFor an isolated parallel plate capacitor of capacitance C and potential difference V, what will be change in (i) charge on the plates (ii) potential difference across the plates (iii) electric field between the plates (iv) energy stored in the capacitor, when the distance between the plates is increased ?
View SolutionFind the total energy stored in the capacitors in the given network.
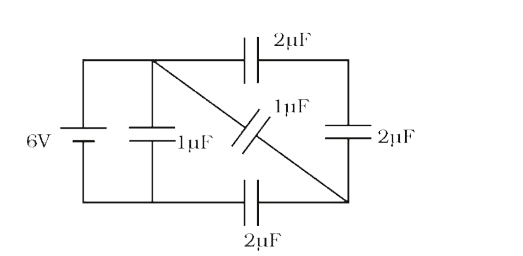
View SolutionWhat happens to the energy stored in a capacitor if after disconnecting the battery, the plates of a charged capacitor are moved farther
View SolutionShown in the figure is network of capacitors & resistors. The potentials of some of the nodes are given. Find the
(a) potential of
(b) energy stored in the capacitor connected between R&S
(c) energy stored in the capacitor connected between P&Q

View SolutionWhat happens to the energy stored in a capacitor if after disconnecting the battery, the plates of a charged capacitor are moved farther
View Solution
