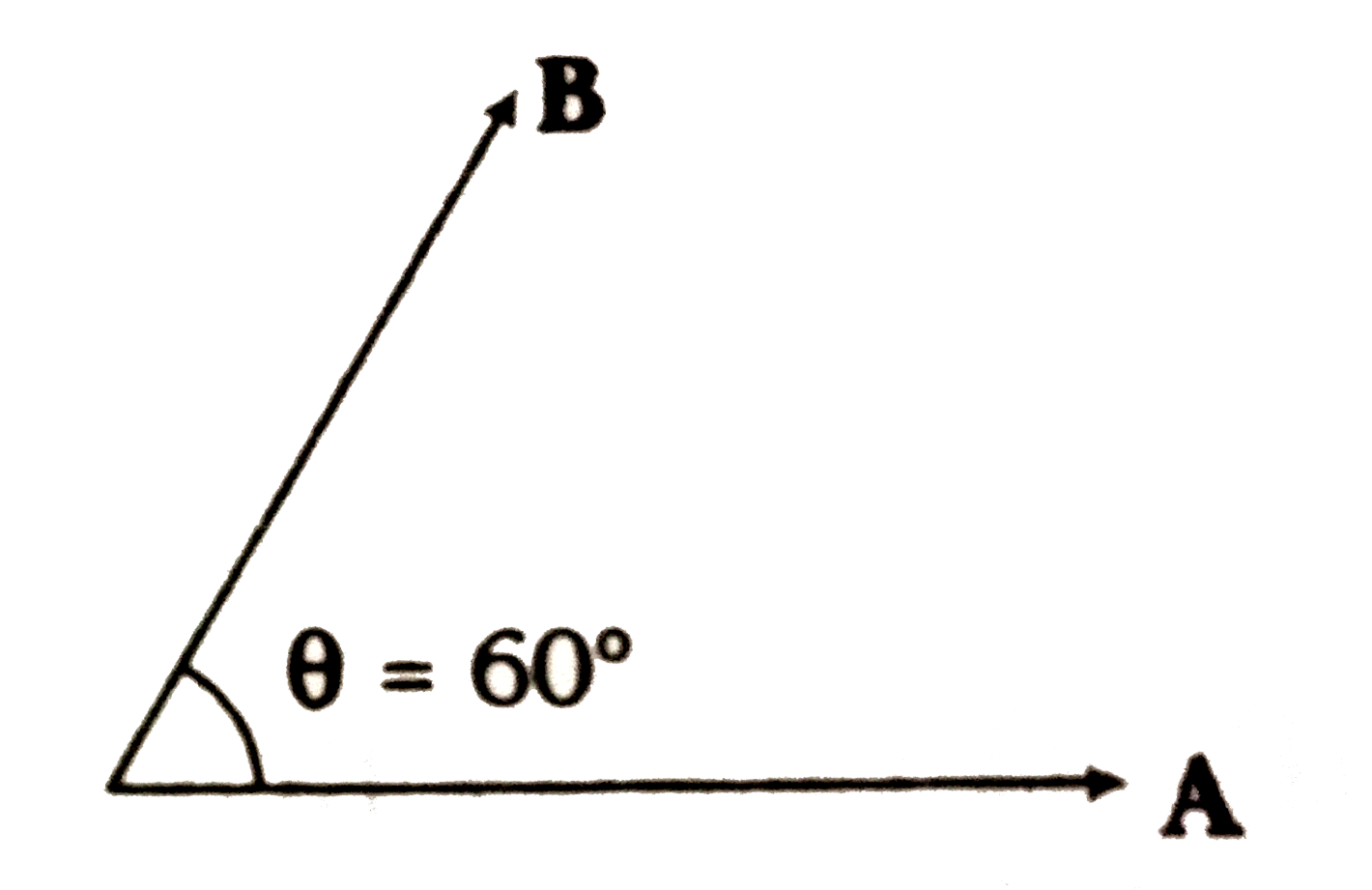
Find the subtraction of vector A and B as shown in thefigure, also find the direction of subtraction vector. Given, A = 4 unit and b = 3 unit.
A
√6 unit,50.1∘
B
√13 unit,46.1∘
C
√3 unit,70∘
D
40 unit, 301∘
Text Solution
(b) According to the question,we draw the following figure

Resultant of the vectors A and B,
R=√A2+B2−2ABcosθ
=√16+9−2×4×3cos60∘
√13 unit ltbr) and direction of the subtraction vector,
tanα=BsinθA−Bcosθ=3sin60∘4−3cos60∘=1.0a
∴α=tan1(1.04)=46.1∘
Thus,A-B is √13 unitat 46.1^(@) from A in the direction shown in figure.
|
Topper's Solved these Questions
- SCALARS AND VECTORS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SCALARS AND VECTORS EXERCISE - Exercise 1
37 Videos
- SCALARS AND VECTORS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SCALARS AND VECTORS EXERCISE - Exercise 2 (Miscellaneous Problems)
20 Videos
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - MHT CET Corner
35 Videos
- SEMICONDUCTORSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEMICONDUCTORSEXERCISE - MHT CET Corner
25 Videos
Similar Questions
Knowledge Check
Find the subraction of vector A and B as shown in the figure , also find the direction of subtraction vector ,Given A=4 unit and b=3 unit .
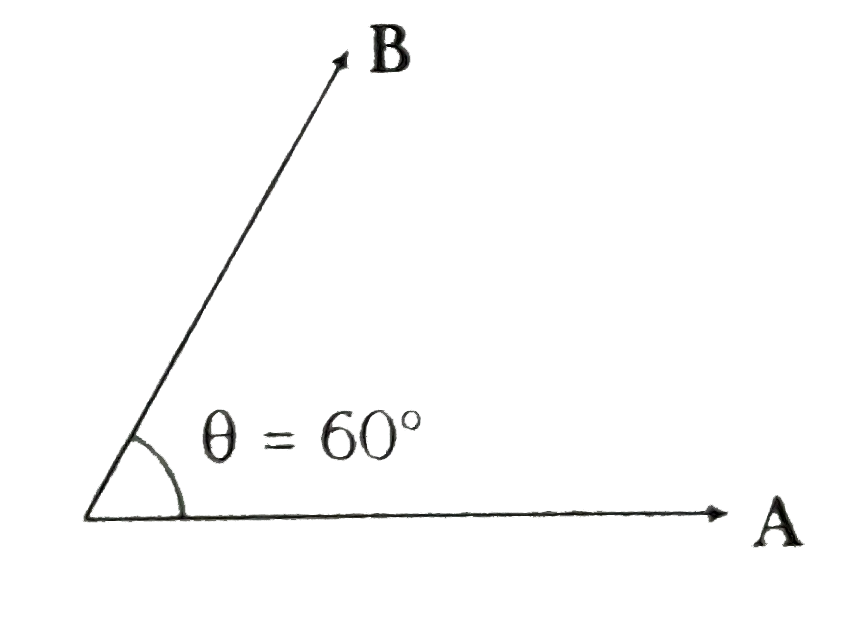 A=√19unit 60B=√24unit 45∘C=√17unit 46.1∘D=√13unit 46.1∘
A=√19unit 60B=√24unit 45∘C=√17unit 46.1∘D=√13unit 46.1∘Find the sum of vector A and B as shown in the figure ,also find the direction of sum vector. Given A=4unit and B=3unit .
 A√35unit , α=tan−1(0.472)=25.3∘B√25unit , α=tan−1(0.472)=25.3∘C√37unit , α=tan−1(0.472)=25.3∘D√37unit , α=tan−1(1)=45∘
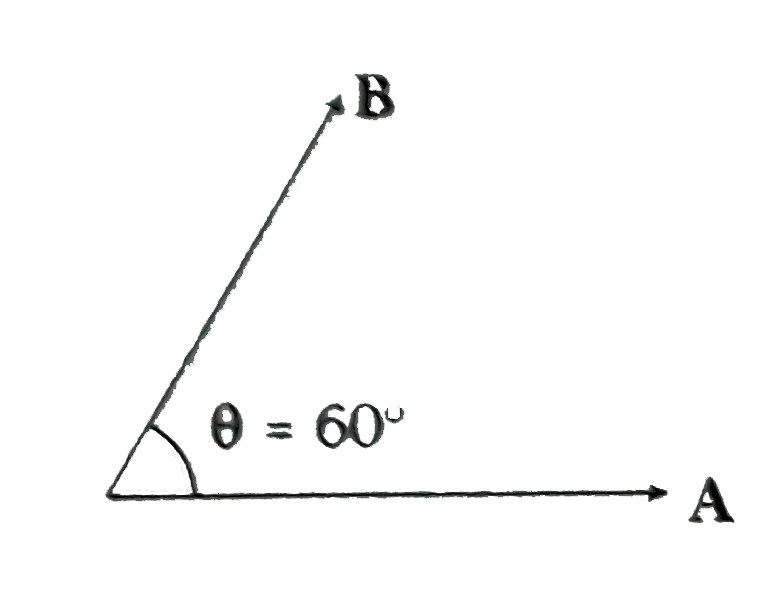
A√35unit , α=tan−1(0.472)=25.3∘B√25unit , α=tan−1(0.472)=25.3∘C√37unit , α=tan−1(0.472)=25.3∘D√37unit , α=tan−1(1)=45∘Find A+B and A-B in the diagram shown in figure. Given A=4 units and B=3 units.
 .A√ 30,√ 22 unitsB√ 40,√ 28C√ 37,√ 15 unitsD√ 37,√ 13
.A√ 30,√ 22 unitsB√ 40,√ 28C√ 37,√ 15 unitsD√ 37,√ 13
Find A+B and A-B in the diagram shown in figure. Given A=4 units and B=3 units.
 .
.
View SolutionFind the unit vector in the direction of the vector →a=ˆi+ˆj+2ˆk.
View SolutionFind the unit vector in the direction of the vector →a=ˆi+ˆj+2ˆk.
View SolutionFind the unit vector in the direction of vector →a=4ˆi+3ˆj+ˆk.
View SolutionFind the unit vector in the direction of vector →a=4ˆi+3ˆj+ˆk.
View Solution
