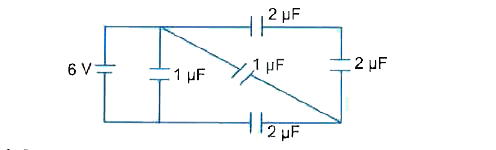
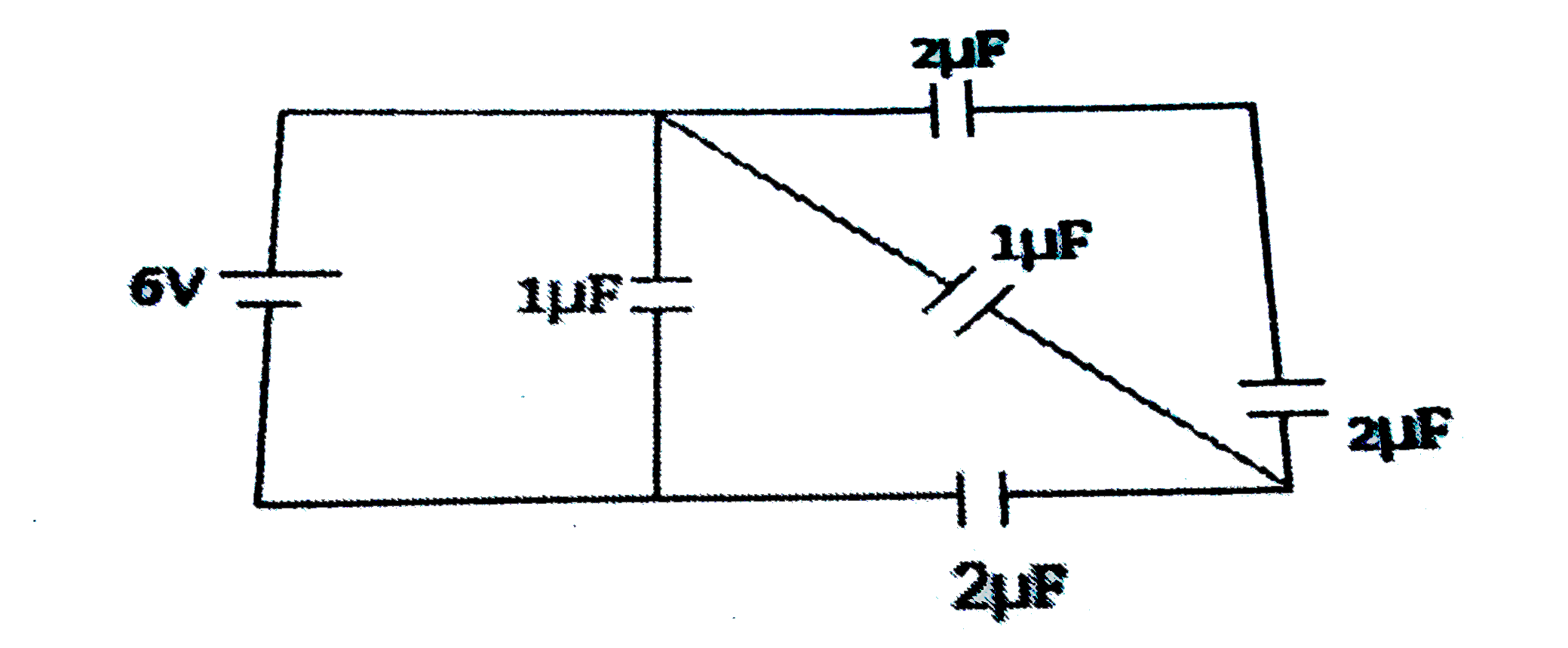
Finding total energy stored in a magnetic field for a length of coaxial cable from the energy density
Finding total energy stored in a magnetic field for a length of coaxial cable from the energy density
(b) What is the stored energy per unit length of the cable if a= 1.2 mm, b = 3.5 mm, and i = 2.7 A?

Video Solution

Text Solution

Verified by Experts

(a) Finding B: To apply these ideas, we begin with Ampere.s law, using a circular path of integration with radius r such that a < r < b (between the two cylinders, as indicated by the dashed line in Fig. 30-32). The only current enclosed by this path is current ion the inner cylinder. Thus, we can write Ampere.s law as
$\int o \vec{B} . d \vec{s} = μ_{0} i$ (30-59)
Next, we simplify the integral: Because of the circular symmetry, at all points along the circular path, $\vec{B}$ is tangent to the path and has the same magnitude B. Let us take the direction of integration along the path as the direction of the magnetic field around the path. Then we can replace $\vec{B} . d \vec{s}$ with B ds $\cos θ = B$ ds and then move magnitude B in front of the integration symbol. The integral that remains is $\int o$ ds, which just gives the circumference 2m- of the path. Thus, Eq. 30-59 simplifies to
$B (2 π r) = μ_{0} i$
or
$B = \frac{μ_{0} i}{2 π r}$ (30-60)
Finding $u_{B}$ : Next, to obtain the energy density, we substitute Eq. 30-60 into Eq. 30-57:
$u_{B} = \frac{B^{2}}{2 μ_{0}} = \frac{μ_{0} i^{2}}{8 π^{2} r^{2}}$ (30-61)
Finding $u_{B}$ : Note that $u_{B}$ is not uniform in the volume between the two cylinders, but instead depends on the radial distance r. Thus, to find the total energy $U_{B}$ stored between the cylinders, we must integrate $u_{B}$ over that volume.
Because the volume between the cylinders has circular symmetry about the cable.s central axis, we consider the volume dV of a cylindrical shell located between the cylinders, the shell has inner radius r, outer radius r + dr (Fig. 30-32), and length l. The shell.s cross-sectional area is the product of its circumference $2 π r$ and thickness dr. Thus, the shell.s volume dV is $(2 π r)$ (dr)(l), that is, dV = $2 π r l$ dr.
Because points within this shell are all at approximately the same radial distance r, they all have approximately the same energy density $u_{B}$ . Thus, the total energy $d U_{B}$ contained in the shell of volume dV is given by
energy =(energy per unit volume)(volume)
or $d U_{B} = u_{B} d V$
Substituting Eq. 30-61 for $u_{B}$ and $2 π r l d r$ for dV, we obtain
$d U_{B} = \frac{μ_{0} i^{2}}{8 π^{2} r^{2}} (2 π r l) d r = \frac{μ_{0} i^{2} l}{4 π} \frac{d r}{r}$
To find the total energy contained between the two cylinders, we integrate this equation over the volume between the two cylinders:
$U_{B} = \int d U_{B} = \frac{μ_{0} i^{2} l}{4 π} \int_{a}^{b} \frac{d r}{r}$
$= \frac{μ_{0} i^{2} l}{4 π} ln \frac{b}{a}$ (30-62)

(b) From Eq. 30-62 we have
$\frac{U_{B}}{l} = \frac{μ_{0} i^{2}}{4 π} ln \frac{b}{a}$
$= \frac{(4 π \times 10^{- 7} J / m) {(2.7 A)}^{2}}{4 π} ln \frac{3.5 m m}{1.2 m m}$
$= 7.8 \times 10^{- 7} J / m = 780 J / m$

Updated on:21/07/2023