Five point masses m each are kept at five vertices of a regular pentagon. Distance of centre of pentagon from any one of the verticle is 'a'. Find gravitational potential and filed strength at centre.
The correct Answer is:A
V=5(−Gma)=−5Gma
For E Five vectors of equal magnitudes, when added as per polygon law of vector. Hence, net E is zero .
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.4
4 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.5
6 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.2
9 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
Knowledge Check
Five point charges, +q each are placed at the five vertices of a regular hexagon. The distance of the center of the hexagon from any fo the vertices is a. the electric field at the center of the hexagon is
Aq4πε0a2Bq8πε0a2Cq16πε0a2DzeroFour point masses each of mass m are placed on vertices of a regular tetrahedron. Distance between any two masses is r.
AGravitation field at centre at zeroBGravitation potential at centre is −4GmrCGravitation potential energy of system in −6Gm2rDGravitation force on one of the point mass is √6Gm2r2Five point charges each of charge + q are placed on five vertices of a regular of side h as shown in the figure. Then
Athe forces on (-q) at O due to charges +q at A and D are balanced.Bthe forces on (-q) due to charges at D and E are balanced.CThe resultant force on −q at O is 14πε0q2h2 along OE.DThe resultant force on - q at O is 14πε0q2h2 along OC.
Four point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
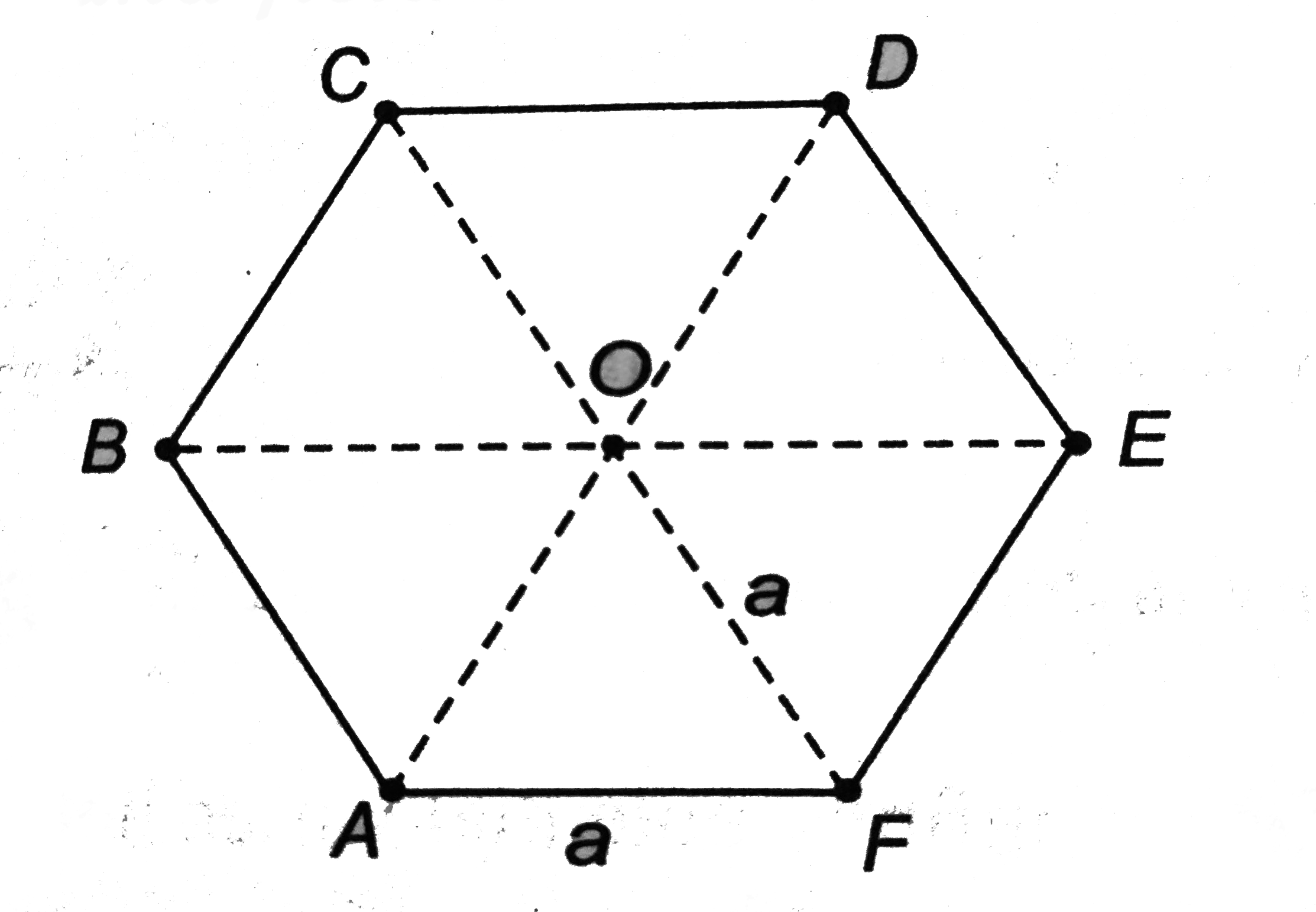 .
.
View SolutionTwo points masses m each are kept at the two verticle of an equaliateral triangle of side 'a' as shows in figure.

Find gravitational potential and magnitude of field strength at O.
View SolutionFive identical charges are kept at five vertices of a regular hexagon. Match the following two columns at centre of the hexagon. If in the given situation electric field at centre is E, then,

View SolutionAssertion : Five charges +q each are placed at five vertices of a regular pentagon. A sixth xharge −Q is placed at the centre of pentagon. Then, net electrostatic force on −Q is zero.
Reason : Net electrostatic potential at the centre is zero.
View SolutionFive charges each q are placed at five corners regular pentagon. Distance from corner to the centre of pontagon is r. Then (K=14πε0)
View Solution
