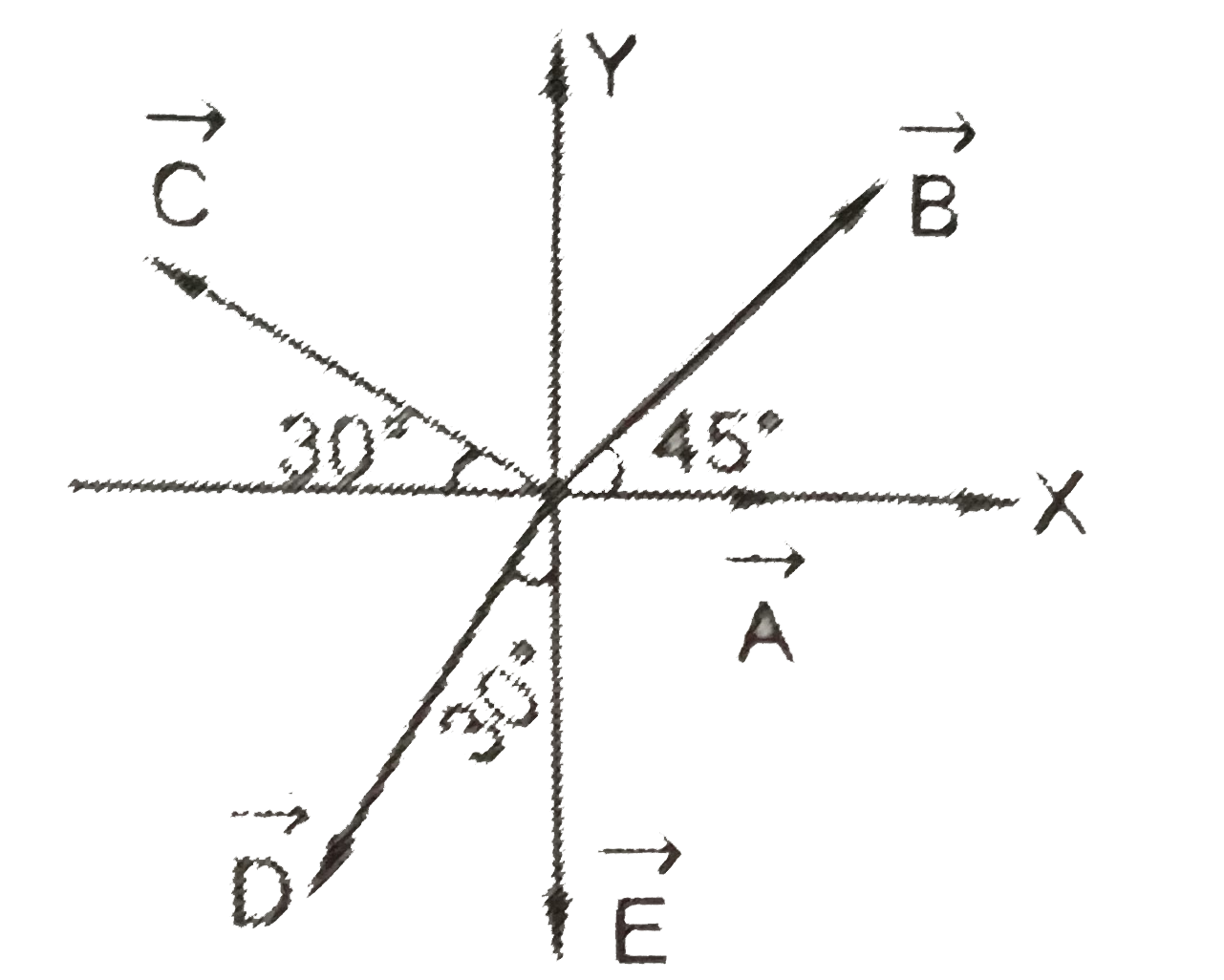
Five vectors →A,→B,→C,→D and →E have magnitude 10,12√2,20,20 and 10 unit respectively, they are direacted as shown in the fig. 3.58
Answer the following questions :
The correct Answer is:C
→A=10ˆi, →B=12ˆi+12ˆj
→C=−√310ˆi+10ˆj , →p=10ˆi−10√3ˆj
→D=−10ˆj
(→A+→C+→D)=−10√3ˆi+(10−10√3)ˆj
x component = −10√3
y component = 10−10√3
Topper's Solved these Questions
Similar Questions
→A,→B and →C are three orthogonal vectors with magnitudes 3, 4 and 12 respectively. The value of ∣∣→A−→B+→C∣∣ will be :-
View SolutionVectors →Cand→D have magnitudes of 3 units and 4 units, respectively. What is the angle between the directions of →Cand→D if →C.→D equals (a) zero, (b) 12 units , and (c ) -12 units ?
View Solution
Knowledge Check
Given : →C=→A+→B . Also , the magnitude of →A,→Band→C are 12,5 and 13 units respectively . The angle between →Aand→B is
A0∘Bπ4Cπ2Dπ→A,→B and →C are three orthogonal vectors with magnitudes 3, 4 and 12 respectively. The value of ∣∣→A−→B+→C∣∣ will be :-
A11B19C13Dcan't be determined
Vectors →Cand→D have magnitudes of 3 units and 4 units, respectively. What is the angle between the directions of →Cand→D if →C.→D equals (a) zero, (b) 12 units , and (c ) -12 units ?
View SolutionThree vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →C
View SolutionThree vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →C
View SolutionThree vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →B
View SolutionIf →a,→b,→c are mutually perpendicular vectors having magnitude 1,2,3 respectively, then [→a+→b+→c,→b−→a,→c]=
View SolutionThe magnitudes of vectors →A,→Band→C are 3,4 and 5 units respectively. If →A+→B=→C, the angle between →A and vecB is
View Solution
