Following are four different relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one (s)

${\to v}_{av} = \frac{1}{2} [\to v (t_{1}) + \to v (t_{2})]$

${\to v}_{av} = (\to r (t_{2})) - \to r \frac{t_{1}}{t_{2} - t_{1}}$

$\to r = \frac{1}{2} (\to v (t_{2}) - \to v (t_{1})) (t_{2} - t_{1})$

${\to a}_{av} = \frac{\to v (t_{2}) - \to v (t_{1})}{t_{2} - t_{1}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C

Which of the following diagrams correctly relate displacement velocity and acceleration with time for a particle executing SHM
A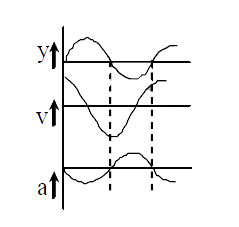
B
C
D
The diplacement , velocity and acceleration in a simple harmonic motion are related as the
Adisplacement , velocity and acceleration all act in the same directionb
Bdisplacement and velocity act in the same direction but acceleration in the opposite direction.
Cvelocity and acceleration are parallel and both are perpendicular to the displacement
Ddisplacement and acceleration are anti-parallel and both perpendicular to the velocity
The phase difference between displacement and acceleration of a particle in a simple harmonic motion is:
A $\frac{3 π}{2}$ rad
B $\frac{π}{2}$ rad
CZero
D $π$ rad