For a fish under water, the entire outside view is confined within a cone. Draw an appropriate ray diagram for this and calculate the value of semi-vertical angle of the cone. Refractive index of water =4/3
To solve the problem of determining the semi-vertical angle of the cone for a fish underwater, we will follow these steps:
Step 1: Understanding the Setup
We have a fish underwater, and we want to visualize the cone of light that it can see. The fish is submerged in water, and the light rays from above the water surface enter the water at different angles.
Step 2: Drawing the Ray Diagram
1. Draw the Water Surface: Start by drawing a horizontal line to represent the water surface.
2. Draw the Fish: Below this line, draw a fish symbol to represent the position of the fish.
3. Indicate the Normal Line: At the point where the light rays enter the water, draw a vertical line (normal) to the water surface.
4. Draw Light Rays: Draw two light rays coming from above the water surface, one at an angle that will refract into the water and one at a steeper angle that will undergo total internal reflection.
5. Label the Angles: Label the angle of incidence (θ) and the critical angle (θc) at the water surface.
Step 3: Applying Snell's Law
To find the critical angle (θc), we can use Snell's Law, which states:
n1sinθ1=n2sinθ2
where:
- n1 is the refractive index of air (approximately 1),
- n2 is the refractive index of water (given as 43),
- θ1 is the angle of incidence,
- θ2 is the angle of refraction.
At the critical angle, the angle of refraction (θ2) is 90 degrees, so we can simplify Snell's Law to:
n1sinθc=n2sin90∘
sinθc=n2n1=143=34
Step 4: Calculating the Critical Angle
Now we can find the critical angle (θc):
θc=sin−1(34)
Using a calculator:
θc≈48.6∘
Step 5: Conclusion
The semi-vertical angle of the cone of vision for the fish underwater is equal to the critical angle, which we calculated to be approximately 48.6∘.
Final Answer
The semi-vertical angle of the cone of vision for the fish is approximately 48.6∘.
---
We have a fish underwater, and we want to visualize the cone of light that it can see. The fish is submerged in water, and the light rays from above the water surface enter the water at different angles.
1. Draw the Water Surface: Start by drawing a horizontal line to represent the water surface.
2. Draw the Fish: Below this line, draw a fish symbol to represent the position of the fish.
3. Indicate the Normal Line: At the point where the light rays enter the water, draw a vertical line (normal) to the water surface.
4. Draw Light Rays: Draw two light rays coming from above the water surface, one at an angle that will refract into the water and one at a steeper angle that will undergo total internal reflection.
5. Label the Angles: Label the angle of incidence (θ) and the critical angle (θc) at the water surface.
To find the critical angle (θc), we can use Snell's Law, which states:
n1sinθ1=n2sinθ2
where:
- n1 is the refractive index of air (approximately 1),
- n2 is the refractive index of water (given as 43),
- θ1 is the angle of incidence,
- θ2 is the angle of refraction.
n1sinθc=n2sin90∘
sinθc=n2n1=143=34
Now we can find the critical angle (θc):
θc=sin−1(34)
θc≈48.6∘
The semi-vertical angle of the cone of vision for the fish underwater is equal to the critical angle, which we calculated to be approximately 48.6∘.
The semi-vertical angle of the cone of vision for the fish is approximately 48.6∘.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (1)
13 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (2)
9 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
Calculate the time taken by light to travel a distance of 10km in water of refractive index 4/3.
View SolutionA salt water lake has refractive index 1.4. A fish when looks towards the surface of water, can only view things outside through a circular area. Calculate the semi-vertical angle of the cone formed within which the circular area lies.
View Solution
Knowledge Check
Brewster angle for air to water transition is (refractive index of water is 43)
Asin−134Bcos−134Ctan−135Dcot−134When the surface of a lake is calm , a fish submerged in water will see the entire outside world within an inverted cone whose vertex is situated at the eye of the fish . What is the vertex angle of the cone ?
(anw=43) and sin49∘=0.75A110∘B98∘C48∘D68∘A diver at a depth of 12 m in water (μ=4/3) sees the sky in a cone of semi-vertical angle
Asin−1(4/3)Btan−1(4/3)Csin−1(3/4)D90∘
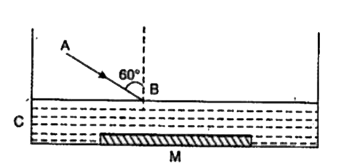
The figure given below shows a container C partially filled with water. There is a plane mirror M at the bottom of the container. A light ray AB incidents on the surface of water at angle of incidence 30∘. Copy and complete the ray diagram. Mark the ray emerging from the water surface. refractive index of water=43.
View SolutionA wooden stick of length 100 cm is floating in water while remaining vertical. The relative density of the wood is 0.7. Calculate the apparent length of the stick when viewed from top (close to the vertical line along the stick) Refractive index of wate =43.

View SolutionA pile 4m high driven into the bottom of a lake is 1m above the <br>water . Determine the length of the shadow of the pile on the bottom of the lake if <br> the sun rays make an angle of 45∘ with the water surface . The refractive index<br> if water is 43.
View SolutionA ray of light propagates from glass (R.I.=32) to water (RI=43) .The value of critical angle
View SolutionIn a lake, a fish rising vertically to the surface of water uniformly at the rate of 3 m/s, observes a bird diving vertically towards the water at the rate of 9 m/s. The actual velocity of the dive of the bird is (given, refractive index of water = 4/3)
View Solution
