For a gas sample with N0 number of molecules, function N(v) is given by : N(v)=dNdv=(3N0v30)v2 for 0<v<v0andN(v)=0 for v>v0, where dN is number of molecules in speed range v to v+dv. Find the rms speed of the molecules.
√53v0
√35v0
√53v0
√35v0
The correct Answer is:B
v2rms=<v2>=v21+v22+v23+....N=∫v2dN∫dN
Here dNdv=N(v),
So, v2rms=1N∞∫0N(v)v2dv=1Nv0∫0(3Nv30.v2)v2dv=35v20
⇒vrms=√35v0
Topper's Solved these Questions
- KINETIC THEORY OF GASES BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)
7 Videos
- KINEMATICS BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE Previous Years Questions (CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )
1 Videos
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
2 Videos
Similar Questions
For a gas sample with N0 number of molecules, function N(V) is given by: N(V)=dNdV=(3N0V30)V2 for 0<V<V0 and N(V)=0 for V>V0. Where dN is number of molecules in speed range V to V+dV. The rms speed of the molecules is:
View SolutionIf speeds of the four molecules of an ideal gas are v, 3v, 5v and 7v respectively, then the mean square speed of the molecules will be
View Solution
Knowledge Check
For a gas sample with N0 number of molecules, function N(V) is given by: N(V)=dNdV=(3N0V30)V2 for 0<V<V0 and N(V)=0 for V>V0. Where dN is number of molecules in speed range V to V+dV. The rms speed of the molecules is:
A√25V0B√35V0C√2V0D√3V0For a gas sample with N0 number of molecules, function N (V) is given by : N(V)=dNdV=(2N0V30)V2 for 0<V<V0andN(V)=0 for V>V0. Where dN is number of molecules in speed range V to V + DV. The rms speed of the molecules is:
A√35V0B√25V0C√2V0D√3V0If vrms is the rms speed of molecules in a gas and v is the speed of sound waves in the gas, then the ratio vrmsv is
A√3γB√γ3C√3γD√3γ
If speeds of the four molecules of an ideal gas are v, 3v, 5v and 7v respectively, then the mean square speed of the molecules will be
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
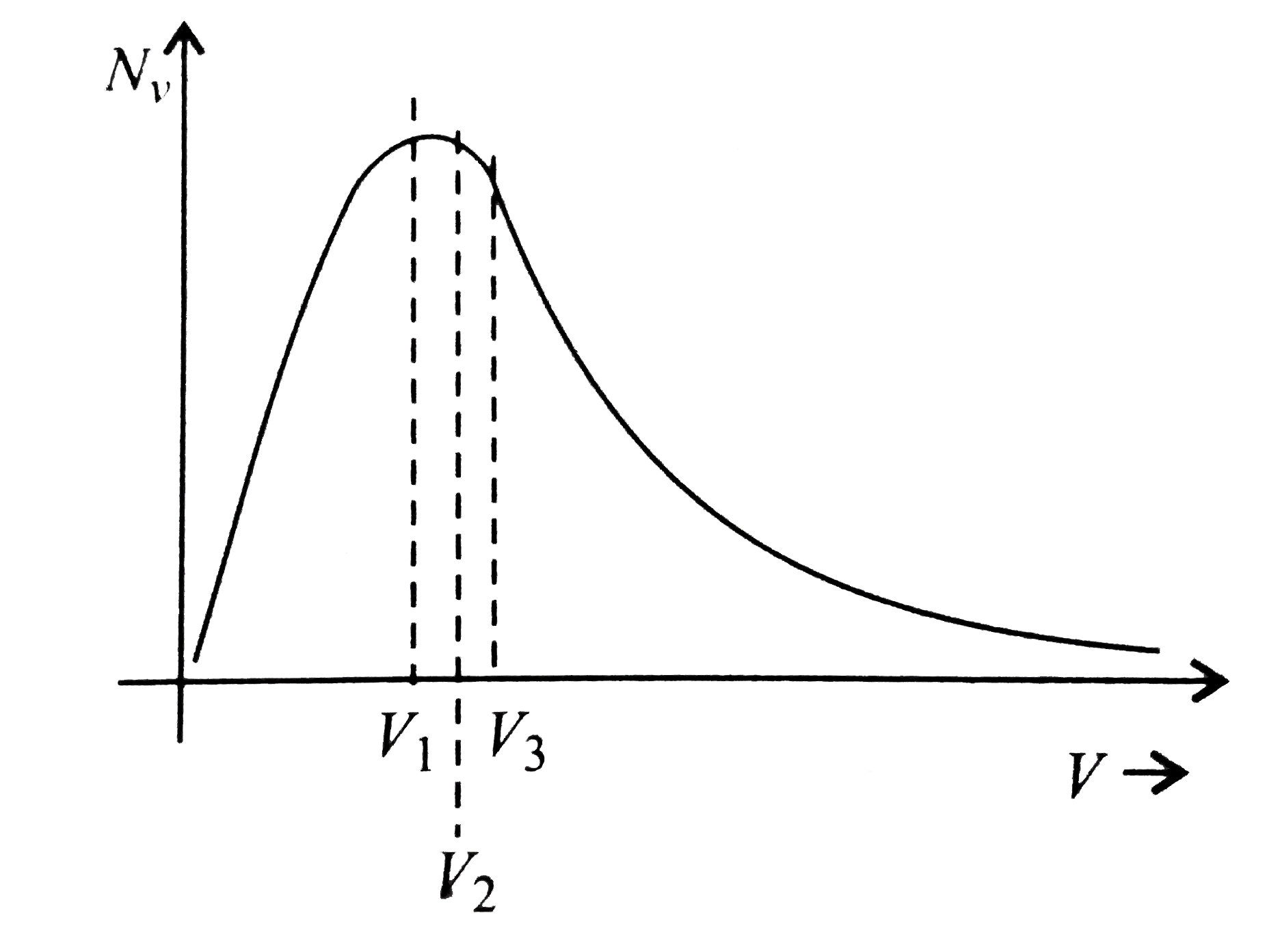
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of a are
View SolutionIf vrms is the rms speed of molecules in a gas and v is the speed of sound waves in the gas, then the ratio vrmsv is
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
If PPc=Pr, TTc=Tr, and VmVm,c=Vr where
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
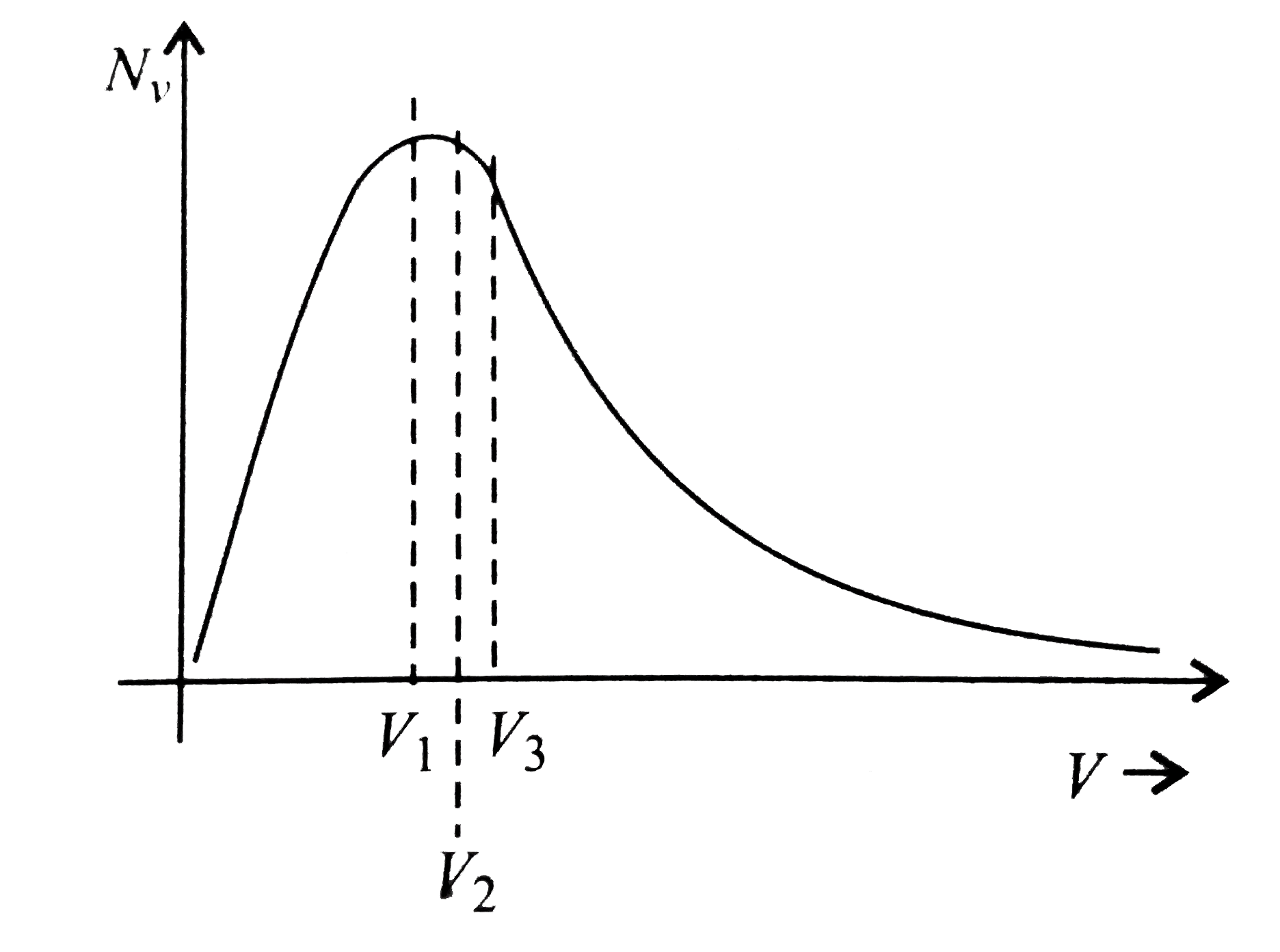
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b are
View Solution
