For a given incident ray, when a plane mirror is turned……….. The reflected ray turns through………. .
an angle θ , and angle 2θ
Topper's Solved these Questions
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - (Test Your Grip)Multiple Choice(sec -A)
1 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
Similar Questions
Knowledge Check
When a plane mirror is rotated through an angle θ then the reflected ray turns through the angle 2θ then the size of the image
AIs doubledBIs halvedCRemins the sameDBecomes infiniteA light ray is incident normally on a plane mirror. The angle of reflection will be
A120∘B90∘C45∘D0∘A ray of light strikes a silvered surface inclined to another one at an angle of 90∘. Then the reflected ray will turn through
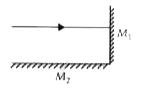 A0∘B45∘C90∘D180∘
A0∘B45∘C90∘D180∘
If the angle of incidence on a plane mirror is 30∘, then angle between the reflected ray and the plane mirror is _____
View SolutionFor a fixed incident light ray, if the mirror be rotated through and angle θ (about an axis which lies in the plane of mirror and perpendicular to the plane of incidence), show that the reflected ray turns through an angle 2θ in same sense.
View SolutionIf a plane mirror is rotated in its ownplane through an angle of 20° keeping the incident ray direction fixed, then the angle through which the reflected ray turns is
View SolutionIf angle fo incidence of a light ray on a plane mirror is 30∘ , then
View SolutionRead the following statements and choose the correct option.
(A) The angle made by the incident light ray with the plane of mirror is equal to the angle made by the reflected light ray with the plane of mirror.
(B) The angle between an incident light ray and a reflected light ray is twice that of the angle between the incident light ray and normal.
View Solution
