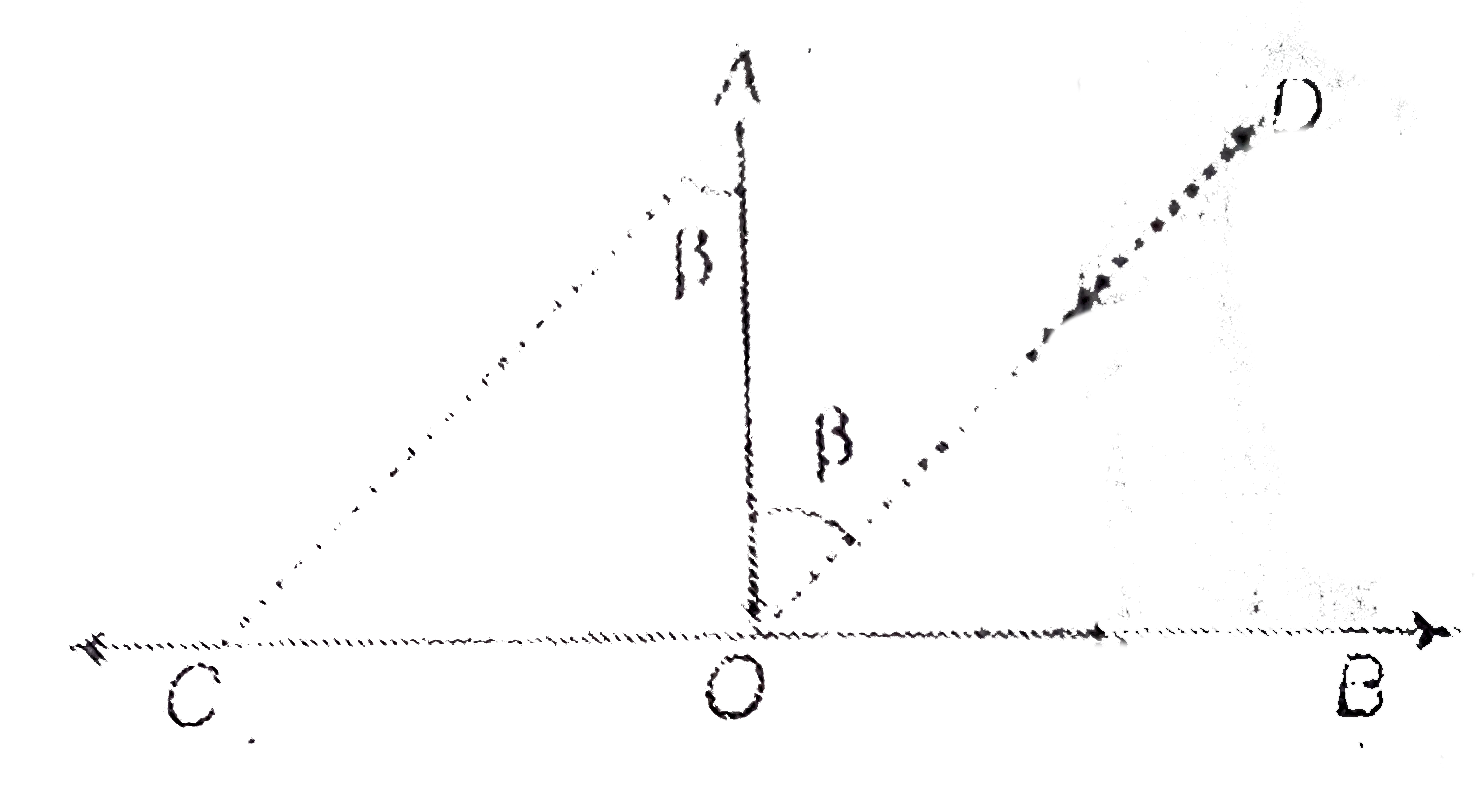
For a man who wants to cross the river, with the shortest path AB, find the anglet θ (see figure)
sin−1(34)
sin−1(43)
30∘
Given situation is not possible
(d) For the man to cross the river frm the shortest path,
Vmsinθ=vr
sinθ=vrvm
sinθ=43
θ=sin−1(/3)
But it is not possible, because sinθ could not be greater than t. Hence the man could not cross the river from the shortest path AB.
Topper's Solved these Questions
Similar Questions
The velocity of a boat in still water is 10 m/s. If water flows in the river with a velocity of 6 m/s what is the difference in times taken to cross the river in the shortest path and the shortest time. The width of the river is 80 m.
View SolutionVelocity of boat in still water is 13 m/s. If water flows ina river with a velocity of 5 m/s. What is the difference in times taken by him to cross the river in the shortest path and in the shortest time. If the width of the river is 10 m.
View Solution
Knowledge Check
The velocity of a boat in still water is 10m/s.If water flows in the river with a velocity of 6m/s what is the difference in times taken to cross the river in the shortest path and the shortest time.The width of the river is 80m.
A1sB10sC√32sD2sman wants to swim across a river of which 200 m along the shortest path . If the speed of river stream is 3kmh−1 and speed of swimmer in still water is 5kmh−1 , then the time of crossing the river is
A10 minB15 minC3 minD6 minA river flows with a speed more than the maximum speed with which a person can swim in still water. He intends to cross the river by the shortest possible path (i.e., he wants to reach the point on the opposite bank which directly opposite to the starting point). Which of the following is correct ?
AHe should normal to the river bank.BHe should start in such a way that he moves normal to the bank, relative to the bank.CHe should start in a particular (calculated) direction making an obtuse angle with the direction of water current.DThe man cannot cross the river in that way.
man wants to swim across a river of which 200 m along the shortest path . If the speed of river stream is 3kmh−1 and speed of swimmer in still water is 5kmh−1 , then the time of crossing the river is
View SolutionA river flows with a speed more than the maximum speed with which a person can swim in still water. He intends to cross the river by the shortest possible path (i.e., he wants to reach the point on the opposite bank which directly opposite to the starting point). Which of the following is correct ?
View SolutionA man can swim at the rate of 5kmh−1 in still water. A 1−km wide river flows at the rate of 3kmh−1 The man wishes to swim across the river directly opposite to the starting point.
(a) Along what direction must the man swim ?
(b) What should be his resultant velocity ?
( c) How much time will he take to cross the river ?
View Solution2 km wide river flowing with a rate of 5 km/hr. A man can swim in the still water with10 km/hr. He wants to cross the river along shortest path find
In which direction person should be swim
View SolutionA person, intending to cross a river by the shortest path, starts at an angle ∝ with the downstream. If the speed of the person be less than that of water current, show that ∝ must be obtuse.
View Solution
