For a particle under going rectilinear motion with uniform acceleration, the magnitude of displacement is one third the distance covered in some time interval. The magnitude of final velocity is less than magnitude of initial velocity for this time interval. Then the ratio of initial speed velocity to the final speed for this time interval is :

A

$\sqrt{2}$

B

2

C

$\sqrt{3}$

D

3

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

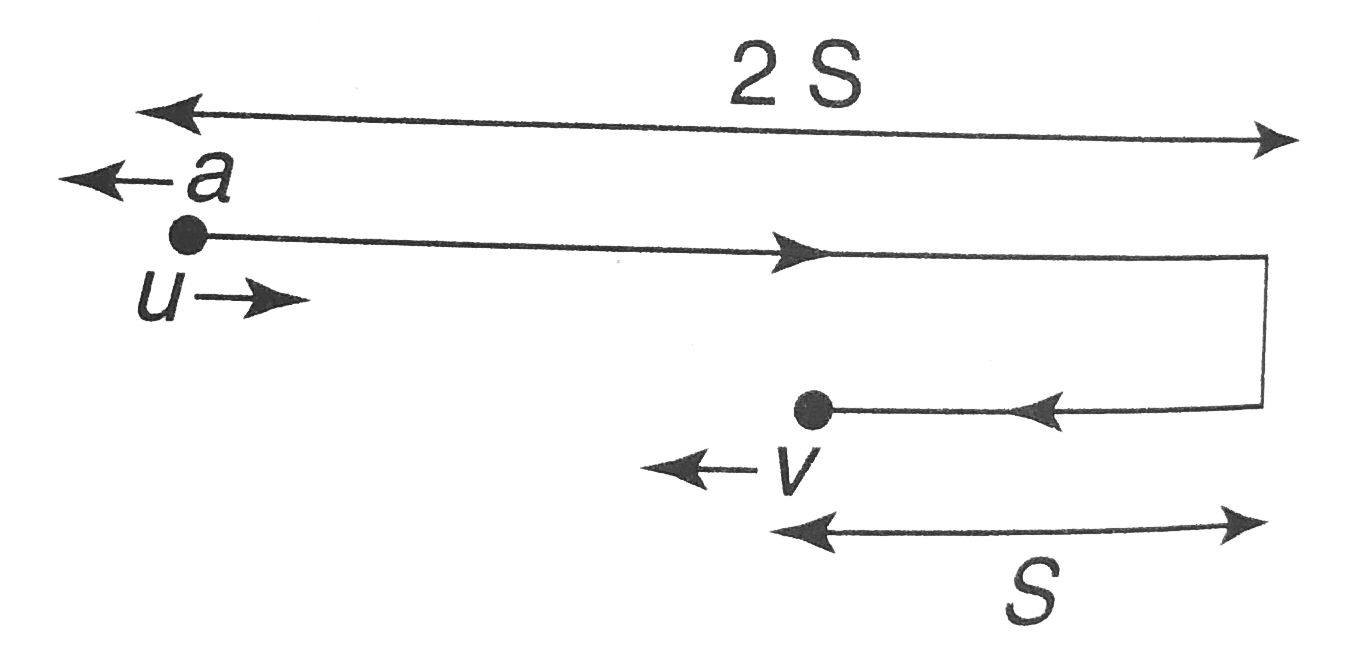
Let $u and v$ denote initial and final velocities. The nature of motion is indicated in diagram.
Hence initial and final speeds are given by equation
$0^{2} = u^{2} - 2 a \times 2 S$ and $v^{2} = 0^{2} + 2 a s$
$∴ v = \frac{u}{\sqrt{2}}$ or $\frac{u}{v} = \sqrt{2}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A point traversed 3/4 th of the circle of radius R in time t. The magnitude of the average velocity of the particle in this time interval is
A $\frac{π R}{t}$
B $\frac{3 π R}{2 t}$
C $\frac{R \sqrt{2}}{t}$
D $\frac{R}{\sqrt{2} t}$
Question 2 - Select One
If magnitude of average speed and average velocity over a time interval are same, then
AThe particle must move with zero acceleration
BThe particle must move with non-zero acceleration
CThe particle must be at rest
DThe particle must move in a straight line without turning back
Question 3 - Select One
For body moving with uniform acceleration $a$ , initial and final velocities in a time interval $t$ are $u$ and $v$ respectively. Then its average velocity in the time interval $t$ is
A $(v + a t)$
B $(v - \frac{a t}{2})$
C $(v - a t)$
D $(u - \frac{a t}{2})$

A2Z-GENERAL KINEMATICS AND MOTION IN ONE DIMENSION-Motion With Constant Acceleration

Home
Ask Doubt
Profile