For a two body oscillator system, prove the relation,
T=2π√μk
where, μ=m1m2m1+(m2)= reduced mass.
The correct Answer is:A
A system of two bodies connected by a spring so that both are free to oscillate simple harmonically along the length of the spring constitutes a two body harmonic oscillator.

Suppose, two masses m1 and m2 are connected by a horizontal massless spring of force constant k, so as to be free to oscillate along the length of the spring on a frictionless horizontal surface.
Let l0 be the natural length of the spring and let x1 and x2 be the coordinates of the two masses at any instant of time. Then,
Extension of the spring x=(x1−x2)−l0...(i)
For x>0, the spring force F=kx acts on the two masses in the direction shown in above figure.
Thus, we can write
m1d2x1dt2=−kx...(ii)
m2d2x2dt2=kx ...(iii)
Multiplying Eq. (ii) by m2 and Eq. (iii) by m1 and substracting the latter from the former, we have
m1m2d2x1dt2−m1m2d2x2dt2=−(m2+m1)kx
or m1m2d2(x1−x2)dt2=−kx(m1+m2)
or (m1m2m1+m2)d2dt2(x1−x2)=−kx ...(iv)
Differentiating Eq. (i), twice with respect to time, we have
d2xdt2=d2dt2(x1−x2)
Also, m1m2m1+m2=μ= reduced mass of the two blocks
Substituting these values is Eq. (iv), we have
μd2xdt2=−kx
or μar=−kx
(Here, ar=d2xdt2=d2x1dt2−d2x2dt2 = Relative acceleration)
This, is the standard differential equation of SHM. Time period of which is
T=2π√∣∣∣xar∣∣∣ or T=2π√μk.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 13
3 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Two particles of mass m1andm2 are in space at separation →r [vector from m(1) to m2]. The only force that the two particles experience is the mutual gravitational pull. The force applied by m1onm2is→F. Prove that μd2→rdt2=→F where μm1m2m1+m2 is known as reduced mass for the two particle system .

View SolutionTwo particles having masses m1andm2 are moving with velocities →V1and→V2 respectively. →V0 is velocity of centre of mass of the system.
(a) Prove that the kinetic energy of the system in a reference frame attached to the centre of mass of the system is KEcm=12μV2rel. Where μ=m1m2m1+m2 and Vrel is the relative speed of the two particles.
(b) Prove that the kinetic energy of the system in ground frame is given by
KE=KEcm+12(m1+m2)V20
(c) If the two particles collide head on find the minimum kinetic energy that the system has during collision.
View Solution
Knowledge Check
The period of oscillation of spring pendulum is given by T=2π√mk where m is 100 gm and is know to have 0.1 gm accuracy. The time period is 2 sec. The time of 100 oscillations is measured by a stop watch of least count 0.1 s. The percentage error in k is
A0.1%B1%C0.2%D0.8%The acceleration of system of two bodies over the wedge as shown in figure is (m1=3kg)(m2=5kg)
 A3.39m/s2B4m/s2C1m/s2D2.5m/s2
A3.39m/s2B4m/s2C1m/s2D2.5m/s2Consider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
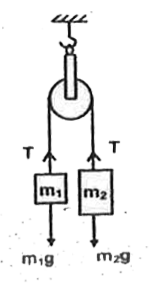
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?A75NB150NC300ND500N
Two blocks of masses m1 and m2 kept touching each other on an inclined plane of inclination a with the horizontal. Show that (i) theforce of interaction between the blocks is (μ1−μ2)m1m2gcosα(m1+m2) and (ii) the minimum value of α at which the blocks just start sliding is a=tan−1.μ1m1+μ2m2m1+m2 . Where μ1 and μ2 are the coefficients of friction between the block m1 and the inclined plane and between the block m2 and the inclinedplane respectively.
View SolutionThere are two blocks of masses m1 and m2,m1 is placed on m2 on a table which is rotating with an angular velocity ω about the vertical axis . The coefficent of friction between the block is μ1 and between m2 and table is μ2(μ1<μ2) if block are placed at distance R from the axis of ratation , for relative sliding between the surface in contact , find the
a. friction force at the contacting surface
b. maximum angular speed ω

View SolutionTwo bodies of masses m1 and m2 are placed at a distance r apart. Show that the position where the gravitational field due to them is zero, the potential is given by
−G(m1+m2+2√m1+m2)/r
View SolutionTwo bodies of masses m1andm2 ar placed at a distance r apart. Shows that the position where the gravitational field due to them is zer, the potential is given by
V=−Gr[m1+m2+2√m1m2]
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
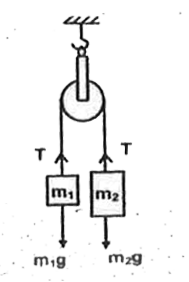
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?
View Solution
