For an LCR series circuit with an aac source of angular frequency ω.
circuit will be capacitive if ω>1√LC
circuit will be inductive if ω=1√LC
Power factor of circuit will be unity if capacitive reactance equals inductive reactance
circuit will be leading voltage if ω>1√LC
The correct Answer is:C
To solve the problem regarding the LCR series circuit with an AC source of angular frequency ω, we will analyze each of the given options step by step.
Step 1: Analyze the condition for a capacitive circuit
- The circuit will be capacitive if the capacitive reactance XC is greater than the inductive reactance XL.
- Mathematically, this can be expressed as:
XC>XL⟹1ωC>ωL
- Rearranging this inequality gives:
ω<1√LC
- Therefore, the first option is correct: The circuit will be capacitive if ω<1√LC.
Step 2: Analyze the condition for an inductive circuit
- The circuit will be inductive if the inductive reactance XL is greater than the capacitive reactance XC.
- This can be expressed as:
XL>XC⟹ωL>1ωC
- Rearranging gives:
ω>1√LC
- Therefore, the second option is correct: The circuit will be inductive if ω>1√LC.
Step 3: Analyze the condition for power factor
- The power factor cosϕ is defined as:
cosϕ=RZ
- The power factor is unity when the impedance Z is equal to the resistance R, which occurs when:
Z=√R2+(XC−XL)2=R
- Squaring both sides gives:
R2+(XC−XL)2=R2⟹(XC−XL)2=0⟹XC=XL
- Therefore, the third option is correct: The power factor of a circuit will be unity if XC=XL.
Step 4: Analyze the condition for leading voltage
- The circuit will have a leading voltage if the capacitive reactance XC is greater than the inductive reactance XL.
- This is the same condition we analyzed in Step 1:
XC>XL⟹1ωC>ωL⟹ω<1√LC
- Therefore, the fourth option is incorrect: The circuit will be leading if ω<1√LC, not ω>1√LC.
Conclusion
After analyzing all four options, we find that:
- Correct Options: A, B, and C
- Incorrect Option: D
Final Answer
The correct answer is that options A, B, and C are correct.
---
- The circuit will be capacitive if the capacitive reactance XC is greater than the inductive reactance XL.
- Mathematically, this can be expressed as:
XC>XL⟹1ωC>ωL
- Rearranging this inequality gives:
ω<1√LC
- Therefore, the first option is correct: The circuit will be capacitive if ω<1√LC.
- The circuit will be inductive if the inductive reactance XL is greater than the capacitive reactance XC.
- This can be expressed as:
XL>XC⟹ωL>1ωC
- Rearranging gives:
ω>1√LC
- Therefore, the second option is correct: The circuit will be inductive if ω>1√LC.
- The power factor cosϕ is defined as:
cosϕ=RZ
- The power factor is unity when the impedance Z is equal to the resistance R, which occurs when:
Z=√R2+(XC−XL)2=R
- Squaring both sides gives:
R2+(XC−XL)2=R2⟹(XC−XL)2=0⟹XC=XL
- Therefore, the third option is correct: The power factor of a circuit will be unity if XC=XL.
- The circuit will have a leading voltage if the capacitive reactance XC is greater than the inductive reactance XL.
- This is the same condition we analyzed in Step 1:
XC>XL⟹1ωC>ωL⟹ω<1√LC
- Therefore, the fourth option is incorrect: The circuit will be leading if ω<1√LC, not ω>1√LC.
After analyzing all four options, we find that:
- Correct Options: A, B, and C
- Incorrect Option: D
The correct answer is that options A, B, and C are correct.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Multiple Correct
5 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Assertion-reasoning
7 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective
15 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
Knowledge Check
A circuit containing a 20Ω resistor and 0.1μF capacitor in series is connected to 320 V ac supply of angular frequency 100 rad s−1. The impedance of the circuit is
A105ΩB104ΩC106ΩD1010Ω
In a series LCR circuit, operated with an ac of angular frequency ω , the total impedance is
View SolutionIn a series LCR circuit with an ac source of 50V,R=300Ω,frequency v=50πHz.The average electric field energy, stored in the capacitor and average magnetic energy stored in the coil are 25mJ and 5mJ respectively.The RMS current in the circuit is 0.10A.Then find
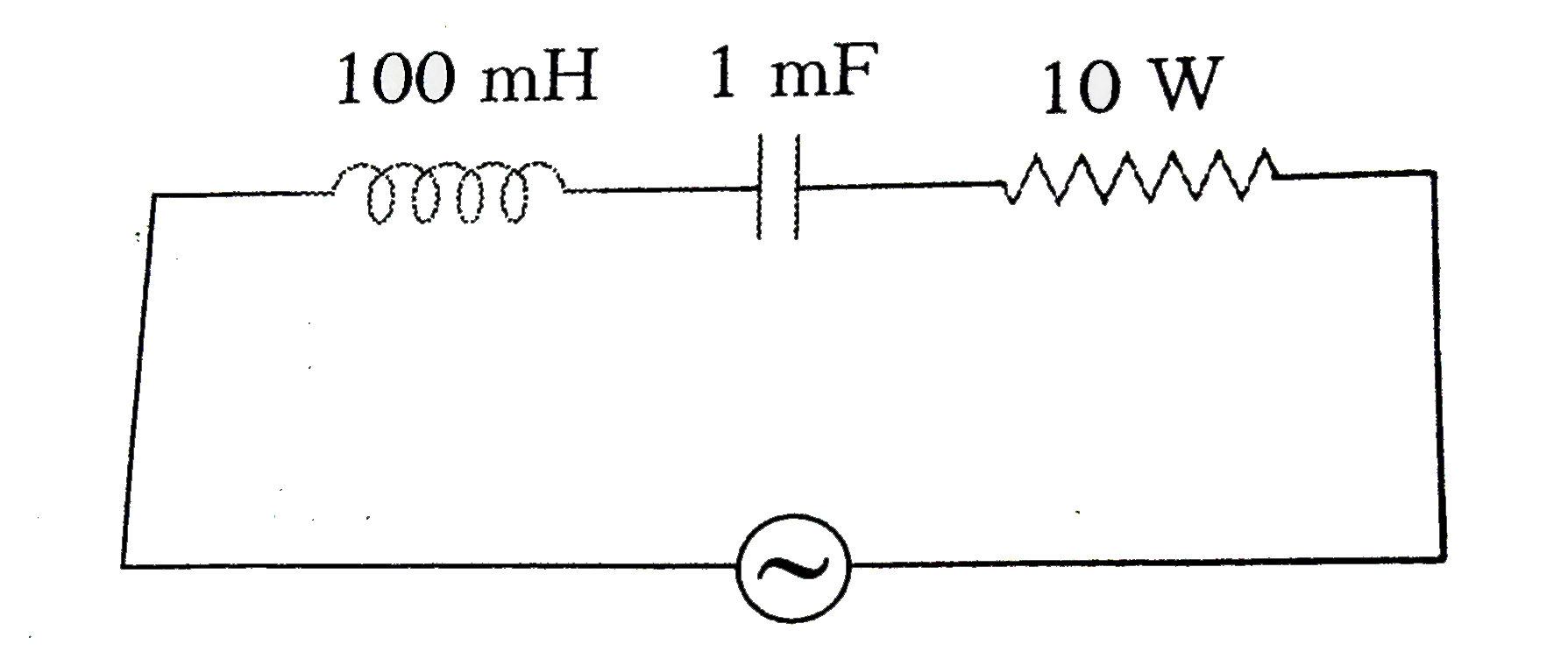
View SolutionThe following series L-C-R circuit , when driven by an emf source of angular frequency 70 kilo-radians per second , the circuit effectively behaves like
View SolutionIn series LCR circuit at resonance
View SolutionA given LCR series circuit satisfes the condition for resonance with a given AC source. If the angular frequency of the AC source is increased by 100% then in order to establish resonance, and without changing the value of inductance, capacitance must be
View SolutionA given LCR series circuit satisfes the condition for resonance with a given AC source. If the angular frequency of the AC source is increased by 100% then in order to establish resonance, and without changing the value of inductance, capacitance must be
View SolutionIn a series LCR circuit connected to an ac source of variable frequency and voltage v=vmsinωt, draw a plot showing the variation of current (I) with angular frequency (ω) for two different values of resistance R1andR2(R1>R2). Write the condition under which the phenomenon of resonance occurs. For which value of the resistance out of the two curves, a sharper resonance is produced ? Define Q-factor of the circuit and give its significance.
View Solution
