For any arbitrary motion in space, which of the following relations are true :-(The ‘average’ stands for average of the quantity over the time interval )Solution in Punjabi
Step by step video & image solution for For any arbitrary motion in space, which of the following relations are true :-v_average=[r(t_2)-r(t_1)/(t_2-t_1)(The ‘average’ stands for average of the quantity over the time interval t_1 to t_2) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A steel wire of length 4.7 m and cross-sectional area 3.0×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0×10−5M2 under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
View SolutionIn which of the following examples of motion, can the body be considered approximately a point object:
View Solutionकिसी दिक्स्थान पर एक स्वेच्छ गति के लिए निम्नलिखित संबंधों में से कौन - सा सत्य है ?
(a) vaverage=(1/2)(v(t1)+v(t2))
(b) vaverage=[r(t2)−r(t1)]/(t2−t1)
(c ) v(t)=v(0)+at
(d) r(t)=r(0)+v(0)t+(1/2)at2
(e) aaverage=[v(t2)−v(t1)]/(t2−t1)
यहाँ 'average ' का आशय समय अंतराल t2 व t1 से संबंधित भौतिक राशि के औसत मान से है |
View SolutionIn the set A of all triangles A, R = { (T_1,T_2):T_1,T_2 Is the relation R defined by
View SolutionWhich of the following statements is correct about the average velocity of a particle? (The average stands for average of the quantity over the time interval , t_1 " to " t_2 )
View SolutionShow that the relation R defined in the set A of all triangles as : R=[(T1,T2):T1andT2 are similar triangles} is an equivalence relation .
View SolutionShow that relation R={(T1,T2): T1 is similar to T2}, defined on the set of all triangles, is an equivalence relation.
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig. 3.29 :-Which of the following formulae are correct for describing the motion of the particle over the time-interval t_1 to t_2 :- x(t_2)=x(t_1)+v(t_1)(t_2-t_1)+(1/2)a(t_2-t_1)^2
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig. 3.29 :- Which of the following formulae are correct for describing the motion of the particle over the time-interval:- vavera≥=x(t2)−x(t1)t2−t1
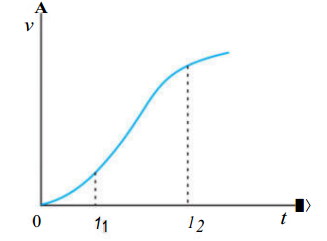
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig. 3.29 :- Which of the following formulae are correct for describing the motion of the particle over the time-interval:- x(t_2)=x(t_1)+v_average(t_2-t_1)+(1/2) a_average(t_2-t_1)^2
View SolutionFor any arbitrary motion in space, which of the following relations are true :- v_average=(1/2) (v(t_1))+(v(t_2)) (The ‘average’ stands for average of the quantity over the time interval t_1 to t_2 )
View SolutionFor any arbitrary motion in space, which of the following relations are true :- v(t)=v(O)+at(The ‘average’ stands for average of the quantity over the time interval t1→t2)
View SolutionFor any arbitrary motion in space, which of the following relations are true :- r(t)=r(O)+v(O)t+(12)at2(The ‘average’ stands for average of the quantity over the time interval t1→t2)
View SolutionFor any arbitrary motion in space, which of the following relations are true :- aaveragv(t2)−v(t1)t2−t1(The ‘average’ stands for average of the quantity over the time interval t1→t2)
View SolutionThe normal drawn at a point (at21,−2at1) of the parabola y2=4ax meets it again in the point (at22,2at2), then t2=t1+2t1 (b) t2=t1−2t1 t2=−t1+2t1 (d) t2=−t1−2t1
View Solution
