For finding the specific resistance of a wire, a student took the following readings by using a metre scale, a micrometer and a resistance box.
Length of the wire (L) = 100.0 cm
Radius (r ) = 0.100 cm and R = 10Ω
What is the maximum possible percentage error in the value of the specific resistance?
9.8%
12.1%
15.5%
18%
The correct Answer is:b
∵R=ρLA
∴ Specific resistance (ρ)=RAL=Rπr2L
∴Δρρ×100=(ΔRR+2Δrr+ΔLL)×100
But ΔR=1Ω,dr=0.001cm,dL=0.1cm
∴(Δρρ)×100=(110+2×0.0010.1+0.1100)×100
=10+2+0.1=12.1%
Topper's Solved these Questions
- MEASUREMENTS BOOK - MARVEL PUBLICATIONCHAPTER - MEASUREMENTS EXERCISE - TEST YOUR GRASP
10 Videos
- MAGNETISMBOOK - MARVEL PUBLICATIONCHAPTER - MAGNETISMEXERCISE - TEST YOUR GRASP
10 Videos
- RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)BOOK - MARVEL PUBLICATIONCHAPTER - RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)EXERCISE - TEST YOUR GRASP
10 Videos
Similar Questions
The specific resistance ρ of a thin wire of radius r cm, resistance R ohm and length L is given by ρ=πr2RL.IfL=78±0.01cm r=0.26±0.02andR=32±1Ω, What is the percentage error in ρ?
View SolutionGiven R1=5.0±0.2Ω,andR2=10.0±0.1Ω. What is the total resistance in parallel with possible % error?
View Solution
Knowledge Check
A wire of length l=±0.06cm and radius r=0.5±0.005cm and mass m=±0.003gm. Maximum percentage error in density is
A(a) 4B(b) 2C( c ) 1D(d) 6.8A wire of length l=6±0.06cm and radius r=0.5±0.005cm and mass m=0.3±0.003g. Maximum percentage error in density is :
A4%B2%C1%D6.8%The radius (r), length (l) and resistance (x) of a thin wire are
(0.2±0.02)cm,(80±0.1)cm, and (30±1)Ω respectively. The percentage error in the specific resistance isA23.4%B25.4%C26%D27.5%
A wire of length l has a resistance R. If half of the length is stretched to make the radius half of its original value, then the final resistance of the wire is
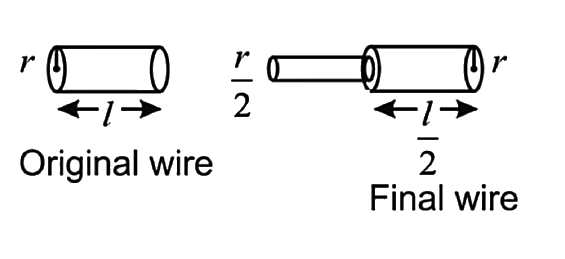
View SolutionA wire of length l=6±0.06cm and radius r=0.5±0.005cm and m=0.3±0.003g. Maximum percentage error in density is:
View SolutionThe resistance of a 5 cm long wire is 10Ω . It is uniformly stretched so that its length becomes 20 cm . The resistance of the wire is
View SolutionThe resistance of a 50 cm long wire is 10Ω. The wire is stretched of uniform wire of length 100 cm. The resistance now will be
View SolutionThe specific resistance of a wire is ρ, its volume is 3m3 and its resistance is 3ohms, then its length will be
View Solution
