For scattering by an .inverse square. field (such as that produced by a charged nucleus in Rutherford.s model), the relation between impact parameter b and the scattering angle θ is given by,
b=Ze2cotθ/24πε0(12mv2)
Why is it that the mass of the nucleus does not enter the formula above but its charge does ?
To understand why the mass of the nucleus does not enter the formula for the impact parameter b in scattering by an inverse square field, we can analyze the situation step by step.
1. Understanding the Formula:
The formula given is:
b=Ze2cot(θ/2)4πϵ0(12mv2)
Here, Z is the atomic number (charge of the nucleus in units of elementary charge), e is the elementary charge, ϵ0 is the permittivity of free space, m is the mass of the alpha particle, v is its velocity, and θ is the scattering angle.
2. Role of Charge:
The interaction causing the scattering is due to the electrostatic force between the positively charged nucleus and the positively charged alpha particle. The strength of this force is directly related to the charge of the nucleus, which is why Z appears in the formula.
3. Assumption of Nucleus at Rest:
In the derivation of this formula, it is assumed that the nucleus is at rest during the interaction. This means that the nucleus does not move significantly when the alpha particle approaches it.
4. Conservation of Momentum:
Since the nucleus is assumed to be at rest, the momentum of the system is primarily carried by the incoming alpha particle. The mass of the nucleus does not affect the trajectory of the alpha particle significantly because it is much more massive than the alpha particle, and thus it does not influence the scattering process.
5. Neglecting Nucleus Mass:
Because the nucleus does not move, its mass does not enter into the calculations of the impact parameter or the scattering angle. The dynamics of the scattering are dominated by the interaction between the charges rather than the masses involved.
6. Conclusion:
Therefore, the formula for the impact parameter b depends on the charge of the nucleus (which determines the strength of the electrostatic interaction) but does not depend on the mass of the nucleus due to the assumption that it remains stationary during the scattering event.
The formula given is:
b=Ze2cot(θ/2)4πϵ0(12mv2)
Here, Z is the atomic number (charge of the nucleus in units of elementary charge), e is the elementary charge, ϵ0 is the permittivity of free space, m is the mass of the alpha particle, v is its velocity, and θ is the scattering angle.
The interaction causing the scattering is due to the electrostatic force between the positively charged nucleus and the positively charged alpha particle. The strength of this force is directly related to the charge of the nucleus, which is why Z appears in the formula.
In the derivation of this formula, it is assumed that the nucleus is at rest during the interaction. This means that the nucleus does not move significantly when the alpha particle approaches it.
Since the nucleus is assumed to be at rest, the momentum of the system is primarily carried by the incoming alpha particle. The mass of the nucleus does not affect the trajectory of the alpha particle significantly because it is much more massive than the alpha particle, and thus it does not influence the scattering process.
Because the nucleus does not move, its mass does not enter into the calculations of the impact parameter or the scattering angle. The dynamics of the scattering are dominated by the interaction between the charges rather than the masses involved.
Therefore, the formula for the impact parameter b depends on the charge of the nucleus (which determines the strength of the electrostatic interaction) but does not depend on the mass of the nucleus due to the assumption that it remains stationary during the scattering event.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - EXERCISE - I20videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - EXERCISE - II19videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - EXERCISE -III25videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (ADVANCED) (Integer Type Questions)2videos
CAPACITORS
Similar Questions
For scattering by an inverse square field (such as that produced by a charged nucleus in Rutherford's model), the relation between impact parameter b and the scattering angle θ is given by,
b=Ze2cotθ/24πε0(12mv2)
What is the impact parameter at which the scattering angle is 90∘ for Z = 79 and initial energy equal to 10MeV ?View SolutionIn Rutherford scattering experiment, wha will be the ratio of impact parameter for scattering angles θ1=90∘andθ2=120∘
View Solution
Knowledge Check
- Question 1 - Select One
For scattering by an inverse-square field (such as that produced by a charged nucleus in Rutherford's model) the relation between impact parameter b and the scattering angle θ is given by, the scattering angle for b=0 is
A180∘B90∘C45∘D120∘
What is the magnitude of a point charge due to which the electric field 30cm away the magnitude 2?
[1/4πε0=9×109Nm2/C2]View SolutionA point charge q is placed on the top of a cone of semi vertex angle θ. Show that the electric flux through the base of cone is q(1−cosθ)2ε0
View SolutionIf ε0 is permittivity of free space, e is charge of proton, G is universal gravitational constant and mp is mass of a proton then the dimensional formula for
e24πε0Gm2p isView SolutionFour similar (+q) are placed at origin O, B, C and D as shown. The angles are as shown. Charges at B, C and D are equidistant from O at a distance of a. The forces of repulsion experienced by charge at O due to charges at B and D along CO are equal, given by q2√38πε0a2. Find the relation between θ1,θ2 and θ3:
 View Solution
View SolutionTwo charges of 4μC each are placed at the corners A and B of an equilaternal triangle of side length 0.2m in air. The
electric potential at C is [14πε0=9×109N−m2C2]View SolutionShow that the magnetic field B at a point in between the plates of a parallel plate capacitor during charging is μ0ε0r2dEdt (symbols having usual meaing). ,
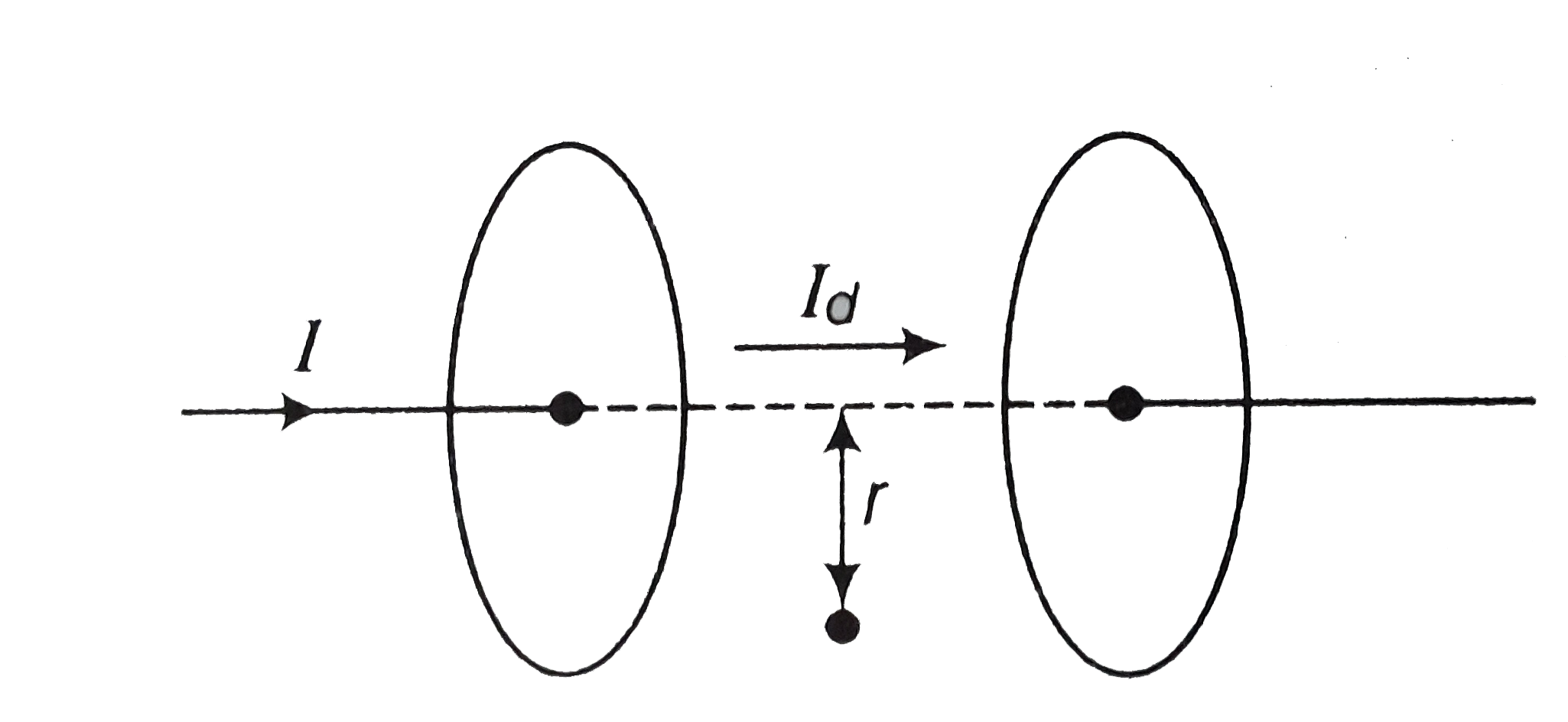 View Solution
View SolutionIf θ is the angle between any two vectors →a and →b , then →a.→b=∣∣→a×→b∣∣ when θ is equal to (a) 0 (B) π4 (C) π2 (d) π
View Solution

