Force acting on a particle constrained to move along x-axis is F=(x−4). Here, F is in newton and x in metre. Find the equilibrium position and state whether it is stable or unstable equilibrium.
The correct Answer is:A, B, D
F=(x−4)
F=0 at x=4m
When x>4m,F=+ve
When displaced from x=4m (towards positive direction) force also acts in the same direction.

Therefpre, equilibrium is unstable.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.5
2 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Introductory
1 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.3
2 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
potential enrgy of a particle along x-axis varies as, U=−20+(x−2)2, where U is in joule and x in meter. Find the equilibrium position and state whether it is stable or unstable equilibrium.
View SolutionPotential energy of a particle moving along x-axis is by
U=(x33−4x+6).
here, U is in joule and x in metre. Find position of stable and unstable equilibrium.
View SolutionA block is constrained to move along x-axis under a force F=−2x. Here, F is in newton and x in metre. Find the work done by this force when the block is displaced fromx=2m→x=-4 m.
View SolutionA block is constrained to move along x-axis under a forc F=4x2(x≠0). Here, F is in newton and x in metre. Find the work done by this force when the block is displaced from x=4 m to x=2m.
View SolutionForce acting on a particle moving along x-axis as shown in figure. Find points of stable and unstable equlibrium.
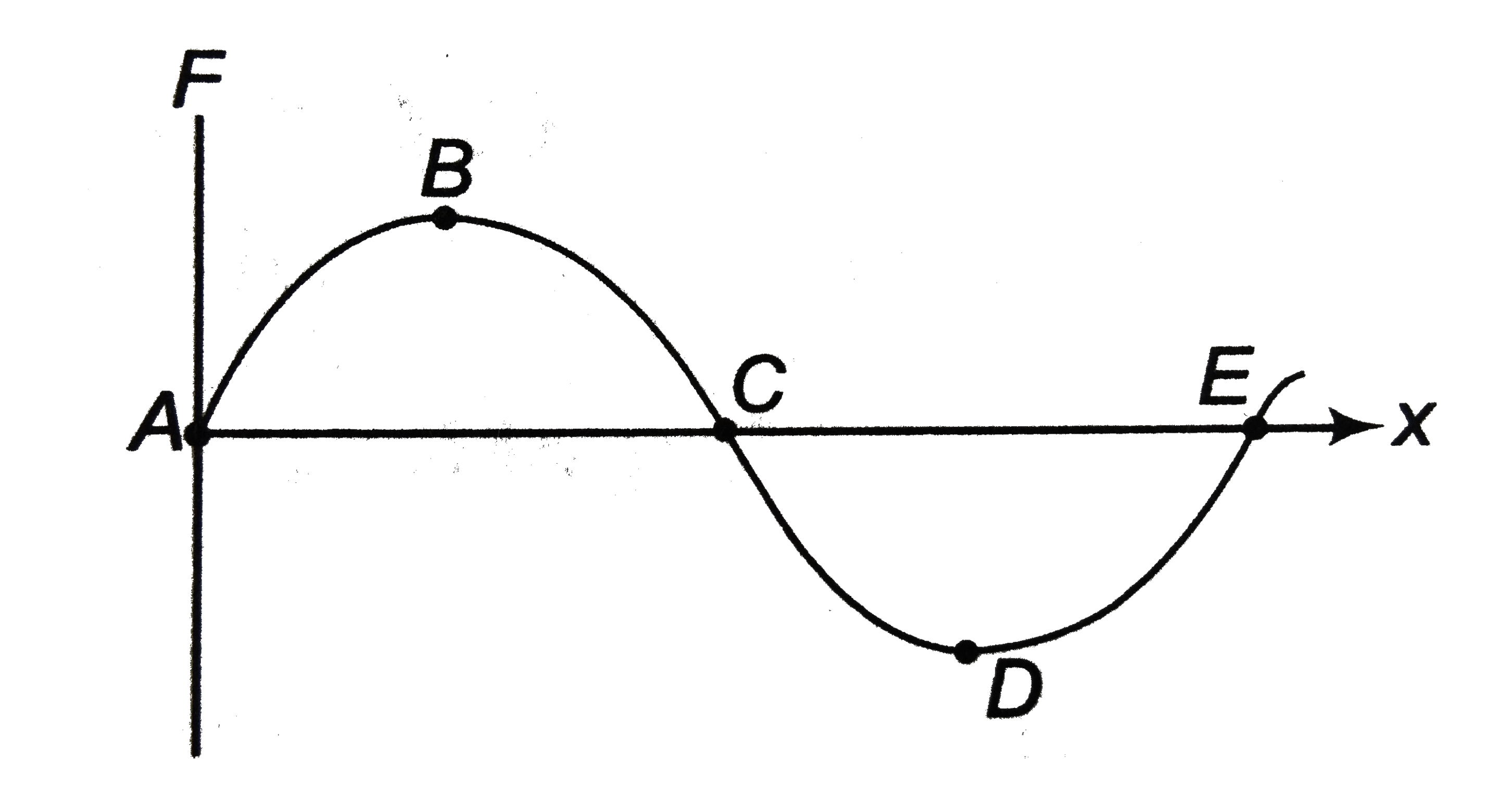 .
.
View SolutionThe potential energy of a conservative force field is given by
U=ax2−bx
where, a and b are positive constants. Find the equilibrium position and discuss whether the equilibrium is stable, unstable or neutral.
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionA force F=(2+x) acts on a particle in x-direction where F is in newton and x in metre. Find the work done by this force during a displacement form 1. 0 m to x = 2.0 m.
View SolutionForce acting on a particle is given by F=A−xBt, where x is in metre and t is in seconds. The dimensions of B is -
View SolutionThe potential energy of a particle oscillating along x-axis is given as
U=20+(x−2)2
Here, U is in joules and x in meters. Total mechanical energy of the particle is 36J.
(a) State whether the motion of the particle is simple harmonic or not.
(b) Find the mean position.
(c) Find the maximum kinetic energy of the particle.
View Solution
