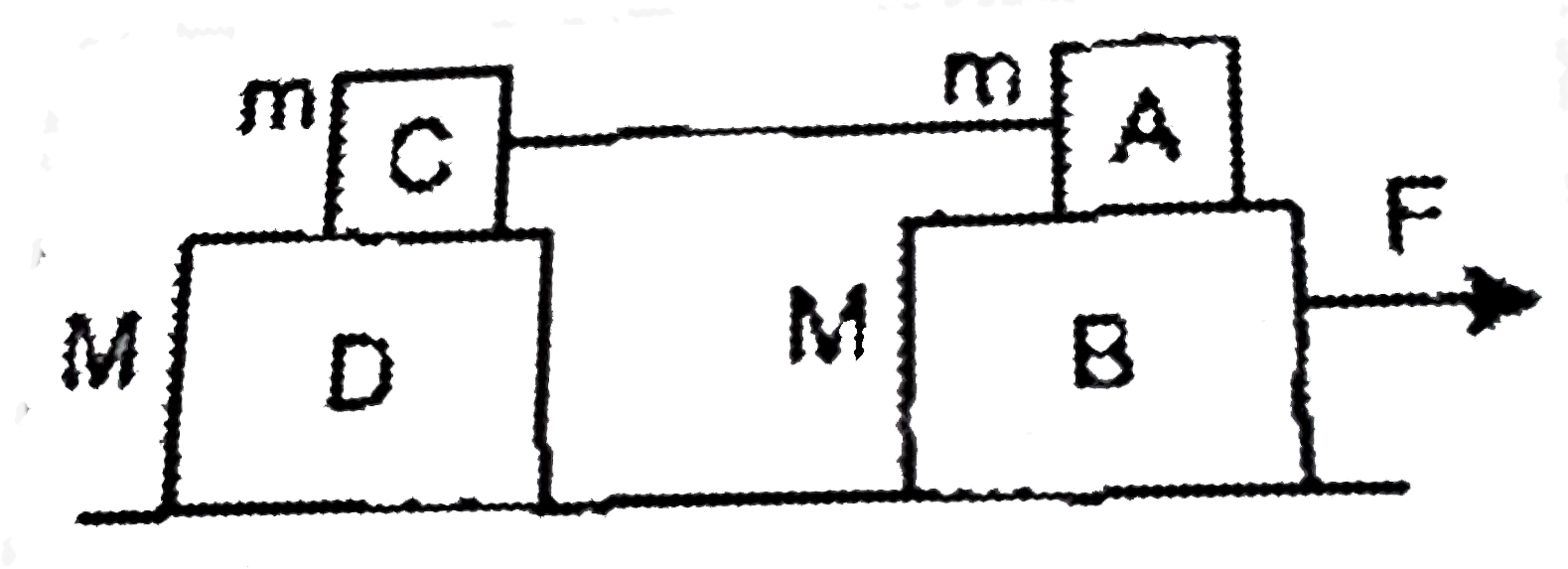
Four block are arranged on a smooth horizontal surface as shown in figure .The masses of the blocks are given (see the fig ) The coefficient of static friction between the top and the bottom blocks is What is the maximum value of the horizontal force applied to one of the bottom blocks as shown that makes all four block with the same acceleration ?

The correct Answer is:C
Let all the four blocks move with a common acceleration acceleration ,
then

Frictionn between C and D will be more than friction between A and B.
Let this friction be then
For no sliping
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE20videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE34videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
Similar Questions
Four blocks are arranged on a smooth horizontal surface as shown. The masses of the blocks are given (see the diagram). The coefficient of static friction between the top and the bottom blocks is μs. What is the maximum value of the horizontal force F, applied to one of the bottom blocks as show, thilt makes all four blocks move with the same acceleration ?
 View Solution
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Coefficient of static friction between the two blocks in Fig. 7.124 is μ and the table is frictionless . Maximum horizontal force which can be applied on the lower such that the blocks move together , is :
 Aμm1gBμm2gCμ(m1−m2)gDμ(m1+m2)g
Aμm1gBμm2gCμ(m1−m2)gDμ(m1+m2)g - Question 2 - Select One
Two identical blocks of weigth w are placed one on top of the other as shown in figure. The upper block is tied to the wall. The coefficient of static friction between B and ground is μ and friction between A and B is absent. When F=μwforce is applied on the lower block as shown. The tension in the string will be
 AμwBμw2C0D2μw
AμwBμw2C0D2μw
Figure shows four blocks that are being pulled along a smooth horizontal surface.The masses of the blocks and tension in one cord are given.The pulling force F is
View SolutionOn a smooth horizontal surface a block A of mass 10kg is kept. On this block a second block B of mass 5kg is kept. The coefficient of friction between the two blocks is 0.4 .A horizontal force of 30N is applied on the lower block as shown. The force of friction between the blocks is
View SolutionA small block of mass 'm' is placed on a plank of mass 'M'. The block is connected to plank with the help of a light string passing over a light smooth pulley as shown in figure. The co-efficient of static friction between the block and plank is μ.
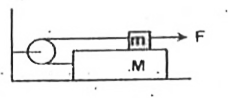
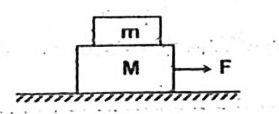
The co-efficient of friction between the plank and the horizontal surface is zero. What maximum horizontal force F applied on the block of mass m can make the block and plank not to slide relatively?View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)
 View Solution
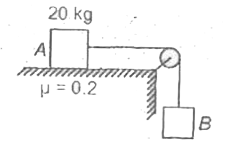
View SolutionIn the figure shown, the coefficient of static friction between the block A of mass 20 kg and horizontal table is 0.2. What should be the minimum mass of hanging block just beyond which blocks start moving?
 View Solution
View SolutionA wooden block of mass m resting on a rough horizontal table is pulled by a force F as shown in the figure. If μ is the coefficient of friction between block and table, its acceleration will be
 View Solution
View Solution

