Four charges +Q,−Q,+Q,−Q are placed at the corners of a square taken in order. At the centre of the square
E=0,V=0
E=0,V≠0
E≠0,V=0
E=0,V≠0
The correct Answer is:A
To solve the problem of finding the electric field and electric potential at the center of a square with charges +Q, -Q, +Q, and -Q placed at its corners, we can follow these steps:
1. Identify the Configuration:
- We have a square with charges placed at its corners in the following order: +Q (top left), -Q (top right), +Q (bottom right), -Q (bottom left).
2. Determine the Position of the Center:
- The center of the square is equidistant from all four charges. Let the distance from the center to any corner of the square be denoted as r.
3. Calculate the Electric Field Due to Each Charge:
- The electric field E due to a point charge Q at a distance r is given by the formula:
E=k|Q|r2
- Here, k is Coulomb's constant.
4. Direction of Electric Fields:
- The electric field due to the positive charges (+Q) will point away from the charge, while the electric field due to the negative charges (-Q) will point towards the charge.
5. Calculate the Electric Field at the Center:
- For the two positive charges (+Q), the electric fields at the center will be directed towards the center from the respective corners, and they will cancel each other out due to symmetry.
- Similarly, for the two negative charges (-Q), their electric fields will also cancel each other out due to symmetry.
6. Net Electric Field:
- Since the electric fields from the positive charges cancel the electric fields from the negative charges, the net electric field at the center of the square is:
Enet=0
7. Calculate the Electric Potential at the Center:
- The electric potential V at a point due to a charge Q is given by:
V=kQr
- The total potential at the center due to all four charges is:
Vtotal=V+Q1+V−Q2+V+Q3+V−Q4
- Substituting the values:
Vtotal=kQr+−kQr+kQr+−kQr
- This simplifies to:
Vtotal=0
8. Conclusion:
- The electric field at the center of the square is zero, and the electric potential at the center is also zero.
Final Answer:
- The electric field at the center is 0 and the electric potential at the center is 0.
- We have a square with charges placed at its corners in the following order: +Q (top left), -Q (top right), +Q (bottom right), -Q (bottom left).
- The center of the square is equidistant from all four charges. Let the distance from the center to any corner of the square be denoted as r.
- The electric field E due to a point charge Q at a distance r is given by the formula:
E=k|Q|r2
- Here, k is Coulomb's constant.
- The electric field due to the positive charges (+Q) will point away from the charge, while the electric field due to the negative charges (-Q) will point towards the charge.
- For the two positive charges (+Q), the electric fields at the center will be directed towards the center from the respective corners, and they will cancel each other out due to symmetry.
- Similarly, for the two negative charges (-Q), their electric fields will also cancel each other out due to symmetry.
- Since the electric fields from the positive charges cancel the electric fields from the negative charges, the net electric field at the center of the square is:
Enet=0
- The electric potential V at a point due to a charge Q is given by:
V=kQr
- The total potential at the center due to all four charges is:
Vtotal=V+Q1+V−Q2+V+Q3+V−Q4
- Substituting the values:
Vtotal=kQr+−kQr+kQr+−kQr
- This simplifies to:
Vtotal=0
- The electric field at the center of the square is zero, and the electric potential at the center is also zero.
- The electric field at the center is 0 and the electric potential at the center is 0.
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Electric Potential Energy
22 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Euipotentials
45 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Four identical charges, Q each, are fixed at the vertices of a square. A free charge q is placed at the centre of the square. Investigate the nature of equilibrium of charge q if it is to be displaced slightly along any of the two diagonals of the square.
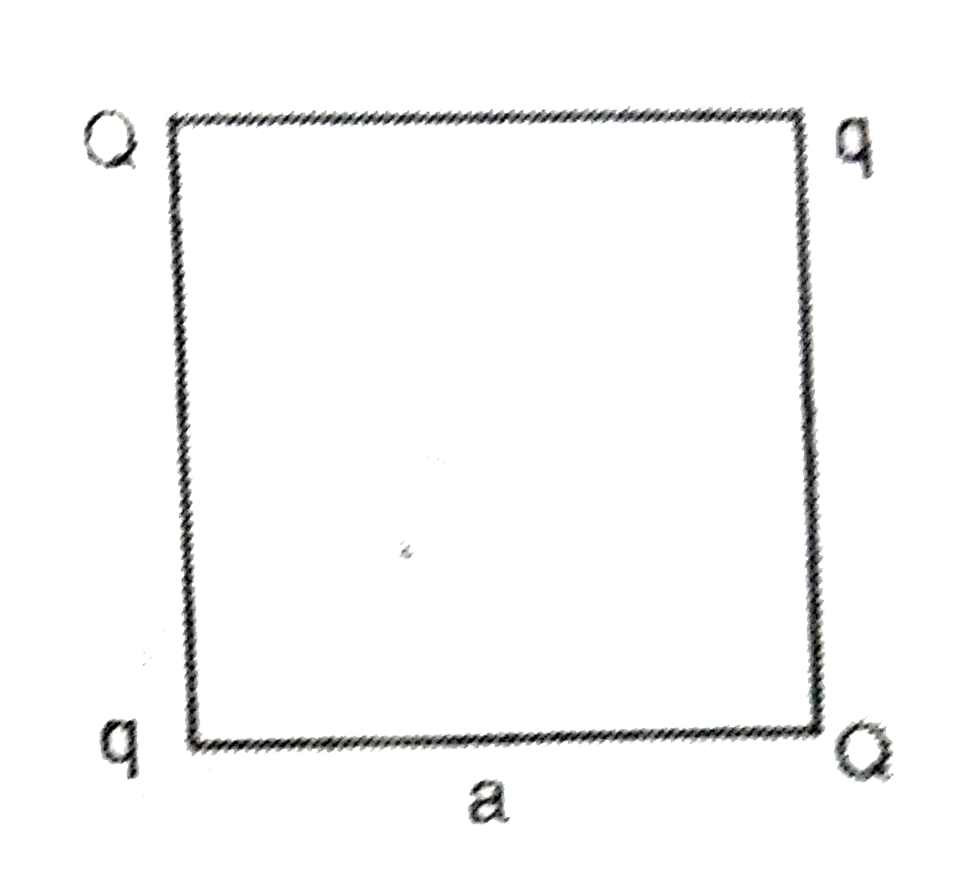
View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
resultant electric force on a charge Q
View Solution
Knowledge Check
Four idential charges each of charge q are placed at the corners of a square .Then at the centre of the square the resultant electric intensity E and the net electric potential V are
AE≠0,V=0BE=0,V=0CE=0,V≠0DE≠0,V≠0Four charges Q-Q, Q-Q are placed at the corners of a square as shown . The potential is zero at points
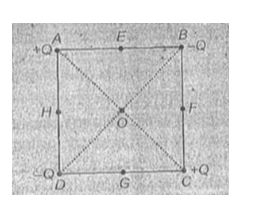 AE,F,G,H,OBE,O,G onlyCH,O,F onlyDO only
AE,F,G,H,OBE,O,G onlyCH,O,F onlyDO onlyFour charges equal to −Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is
A(a) −Q2(1+2√2)B(b) Q4(1+2√2)C(c) −Q4(1+2√2)D(d) Q2(1+2√2)
Four point charges Q, q, Q and q are placed at the corners of a square of side' a' as shown in the figure.
Find the .
(a) resultnat electric force on a charge Q and .
(b) potential energy of this system.
View SolutionFour charges equal to −Q are placed at the four corners of a square and a charge q is at its centre, If the system is in equilibrium the value of q si
View SolutionFour charges equal to Q are placed at the four comers of a square and a charge q is at its centre . If the system is in equilibrium , the value of q is
View Solutionq,2q, 3q and 4q charges are placed at the four corners A,B,C and D of a square. The field at the centre P of the square has the direction parallel to

View SolutionFour electric charges +q,+q,−q and −q are placed at the corners of a square of side 2L (see figure). The electric potential at point A, mid-way between the two charges +q and +q, is

View Solution
