Four equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
4√GMx
√4√2GMx
√8√2GMx
√2GMx
The correct Answer is:C
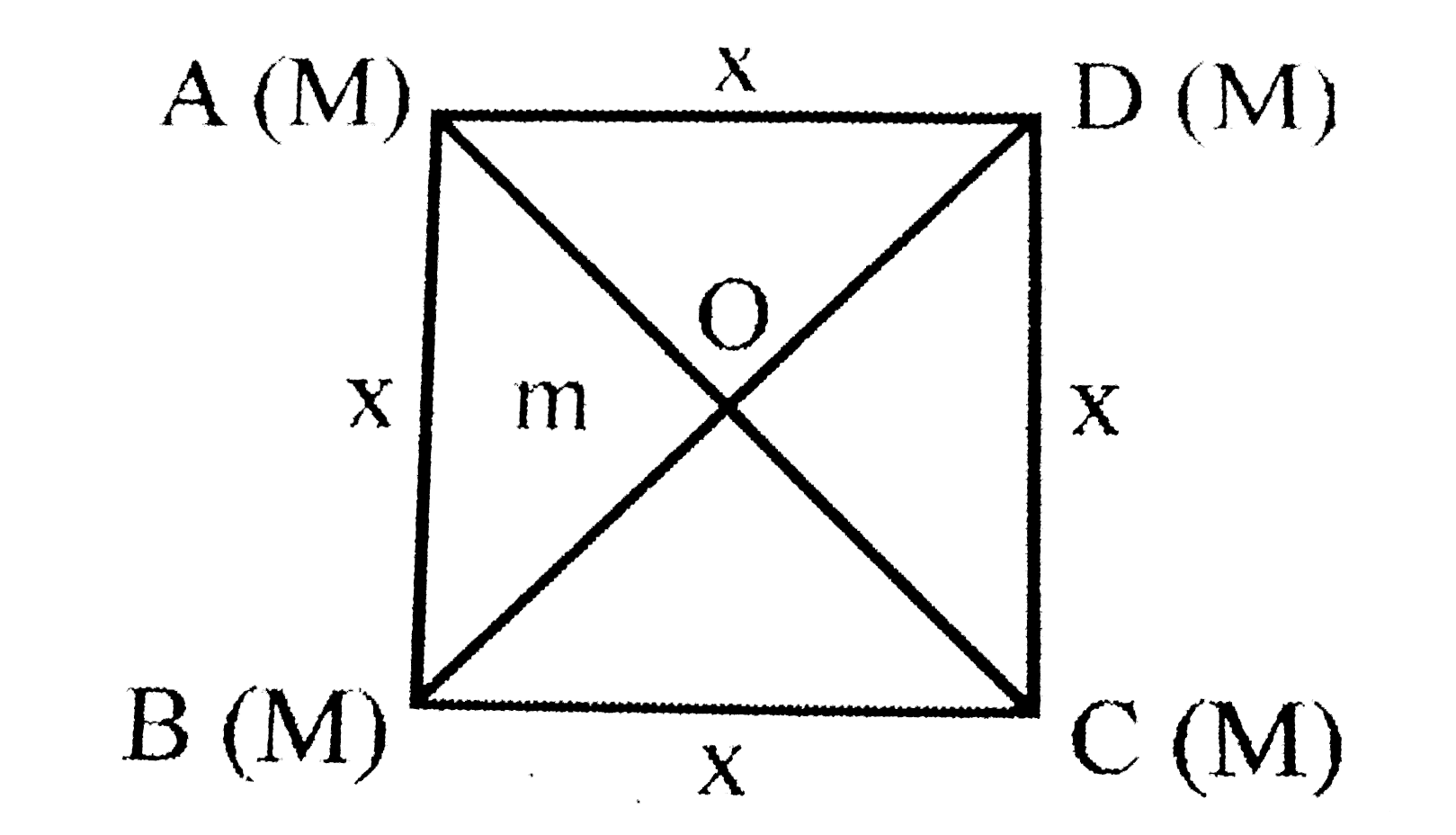
AO=12(AC)=√2x2=x√2
Suppose that a mass m is kept at the centre O.
Potential at the centre O, due to all masses,
vO=4(−GMAO)=−4GMx/√2=−4√2GMx
∴ P.E. of all the masses m (vO)=−4√2GMmx
∴B.E.=+44√2GMmx
∴ If ve is the escape velocity of mass 'm' then
12mv2e=4√2GMmx
∴v2e=8√2GMx ∴ve=√8√2GMx
Topper's Solved these Questions
- GRAVITATION BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -2
20 Videos
- ELECTROSTATICSBOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP
20 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP
20 Videos
Similar Questions
Three equal masses (each m) are placed at the corners of an equilateral triangle of side a. Then the escape velocity of an object from the circumcentre P of triangle is
View SolutionThree equal masses (each m) are placed at the corners of an equilateral triangle of side a'. Then the escape velocity of an object from the circumcentre P of triangle is
View Solution
Knowledge Check
Four equal masses (each of mass M) are placed at the corners of a squares side a the escape velocity of a body from the centre O of the square is
A4√2GMaB√8√2GMaC4GMaD√4√2GMaFour particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−2√2GmlB−3√2GmlC−2GmlD−4√2GmlFour identical charges i.e. q is placed at the corners of a square of side a. The charge Q that must be placed at the centre of the square such that the whole system of charges in equilibrium is
Aq4Bq4[2√2+1]C−q4[2√2+1]D−q4[3√3+1]
Four point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
View SolutionFour particles of masses m, m, 2m and 2m are placed at the four corners of square of side a. Find the centre of mass of the system.
View SolutionFour particles of masses m, m, 2m and 2m are placed at the corners of a square of side a, as shown in fig. Locate the centre of mass.
View SolutionFour particles, each of mass 1kg are placed at the corners of a square of side 1m in the XY plane. If the point of intersecting of the diagonals of the square is taken as the origin, the co-ordinates fo the centre of mass are
View SolutionFour particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis perpendicular to the plane of frame and passing through a corner is
View Solution
