Four identical charges +Q are kept at the corners of a square ABCD. The edge length of square is a . Find net force on the charge kept at C due to the other three charges.
To find the net force on the charge at point C due to the other three charges located at points A, B, and D in a square configuration, we can follow these steps:
Step 1: Identify the forces acting on charge C
The charge at point C experiences forces due to the charges at points A, B, and D. We will denote these forces as:
- FA: Force due to charge at A
- FB: Force due to charge at B
- FD: Force due to charge at D
Step 2: Calculate the magnitudes of the forces
Using Coulomb's law, the magnitude of the force between two point charges is given by:
F=kQ2r2
where k is Coulomb's constant, Q is the charge, and r is the distance between the charges.
- Force FB (between charges B and C):
- Distance r=a
- Magnitude:
FB=kQ2a2
- Force FD (between charges D and C):
- Distance r=a
- Magnitude:
FD=kQ2a2
- Force FA (between charges A and C):
- Distance r=√2a (diagonal of the square)
- Magnitude:
FA=kQ2(√2a)2=kQ22a2
Step 3: Determine the direction of each force
- Force FB acts vertically downward (along the negative y-axis).
- Force FD acts horizontally to the left (along the negative x-axis).
- Force FA acts diagonally towards charge A at an angle of 45 degrees from both axes.
Step 4: Resolve the force FA into components
The components of FA can be resolved as follows:
- FA,x=FAcos(45∘)=kQ22a2⋅1√2=kQ22√2a2
- FA,y=FAsin(45∘)=kQ22a2⋅1√2=kQ22√2a2
Step 5: Sum the forces in the x and y directions
- Net force in the x-direction:
Fnet,x=−FD+FA,x=−kQ2a2+kQ22√2a2
- Net force in the y-direction:
Fnet,y=−FB+FA,y=−kQ2a2+kQ22√2a2
Step 6: Combine the forces to find the net force
The net force vector →Fnet can be expressed as:
→Fnet=Fnet,x^i+Fnet,y^j
Step 7: Calculate the magnitude of the net force
The magnitude of the net force is given by:
Fnet=√F2net,x+F2net,y
Step 8: Determine the direction of the net force
The angle θ of the net force can be determined using:
tan(θ)=Fnet,yFnet,x
Final Result
The net force on charge C due to the other three charges can be expressed in terms of k, Q, and a as derived above.
---
The charge at point C experiences forces due to the charges at points A, B, and D. We will denote these forces as:
- FA: Force due to charge at A
- FB: Force due to charge at B
- FD: Force due to charge at D
Using Coulomb's law, the magnitude of the force between two point charges is given by:
F=kQ2r2
where k is Coulomb's constant, Q is the charge, and r is the distance between the charges.
- Distance r=a
- Magnitude:
FB=kQ2a2
- Distance r=a
- Magnitude:
FD=kQ2a2
- Distance r=√2a (diagonal of the square)
- Magnitude:
FA=kQ2(√2a)2=kQ22a2
- Force FB acts vertically downward (along the negative y-axis).
- Force FD acts horizontally to the left (along the negative x-axis).
- Force FA acts diagonally towards charge A at an angle of 45 degrees from both axes.
The components of FA can be resolved as follows:
- FA,x=FAcos(45∘)=kQ22a2⋅1√2=kQ22√2a2
- FA,y=FAsin(45∘)=kQ22a2⋅1√2=kQ22√2a2
- Net force in the x-direction:
Fnet,x=−FD+FA,x=−kQ2a2+kQ22√2a2
- Net force in the y-direction:
Fnet,y=−FB+FA,y=−kQ2a2+kQ22√2a2
The net force vector →Fnet can be expressed as:
→Fnet=Fnet,x^i+Fnet,y^j
The magnitude of the net force is given by:
Fnet=√F2net,x+F2net,y
The angle θ of the net force can be determined using:
tan(θ)=Fnet,yFnet,x
The net force on charge C due to the other three charges can be expressed in terms of k, Q, and a as derived above.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Practice Problems
88 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Four identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View Solution
Knowledge Check
Four charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the ccentre O is
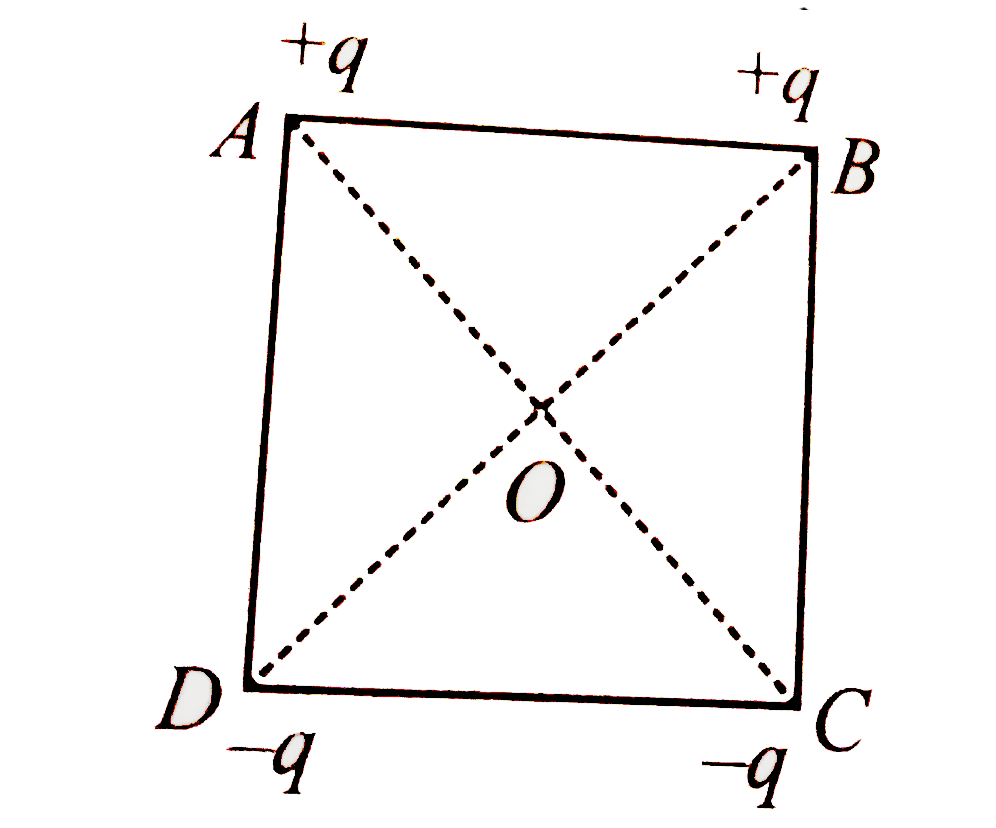 Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB
Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side ABA point charge q is kept at a corner of a cube
AElectric flux linked with individual faces of the cube may be zeroBElectric flux linked with individual faces of the cube may be non-zeroCElectric flux linked with a certain face of the cube may be q/8ε0DElectric flux linked with a certain face of the cube may be q/24ε0Four charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:
 Aperpendicular to side ABBalong the diagonal BDCalong the diagonal ACDzero
Aperpendicular to side ABBalong the diagonal BDCalong the diagonal ACDzero
Four charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:

View SolutionFour charges are arranged at the corners of a square ABCD, as shown. The force on a =ve charge kept at the centre of the square is -

View SolutionFour charges are arranged at the corners of a square ABCD, as shown in the adjoining figure, The force on a positive charge kept at the centre O is
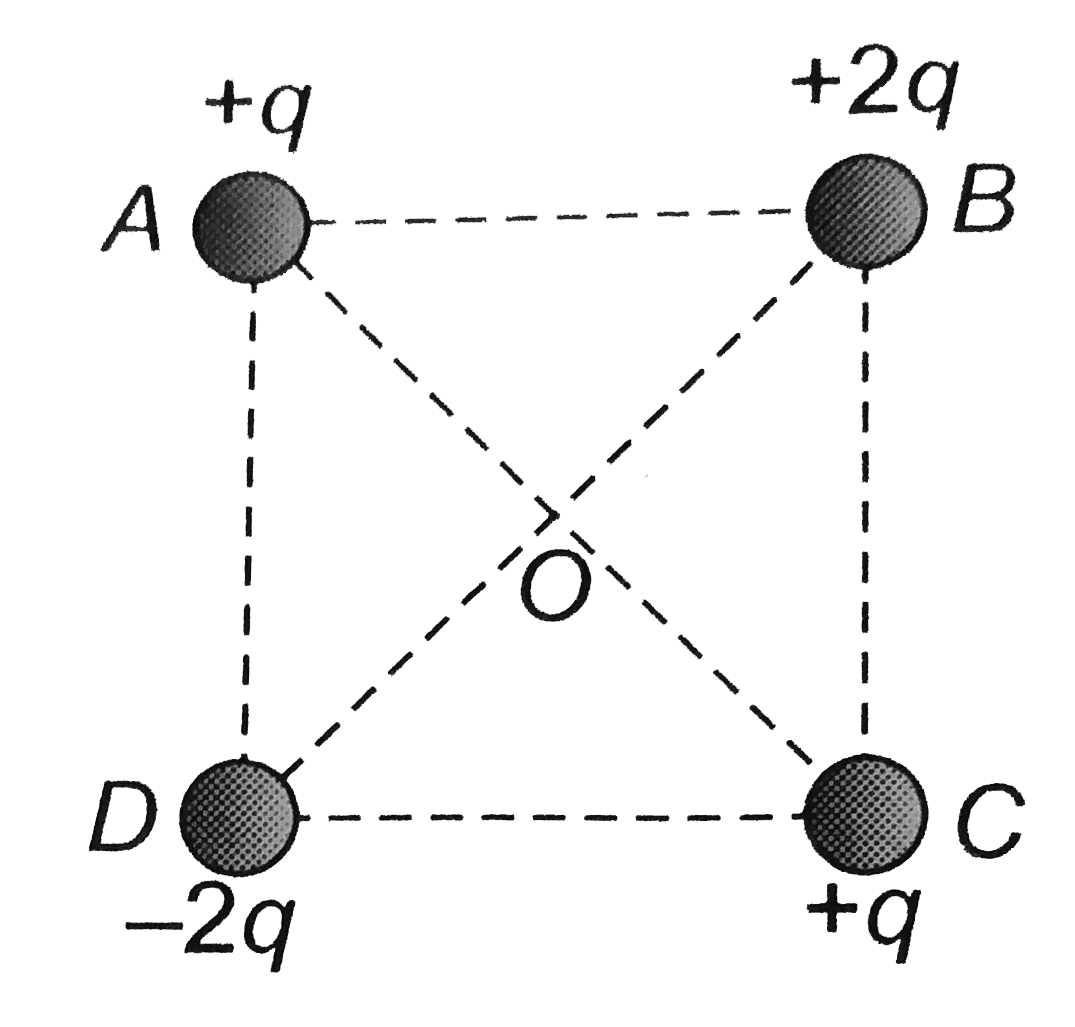
View SolutionEqual charges q are placed at the four corners A,B,C,Dof a square of length a. The magnitude of the force on the charge at B will be
View SolutionEqual charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
View Solution
