Four point masses, each of value m, are placed at the corners of a squre ABCD of side l. The moment of inertia of the is system about an axis passing through A and parallel to BD is
2ml2
√3ml2
3ml2
ml2
The correct Answer is:C
To find the moment of inertia of the system of four point masses located at the corners of a square about an axis passing through point A and parallel to the diagonal BD, we can follow these steps:
Step 1: Understand the Configuration
We have four point masses, each of mass m, located at the corners of a square ABCD with side length l. The points are:
- A at (0, 0)
- B at (l, 0)
- C at (l, l)
- D at (0, l)
Step 2: Identify the Axis of Rotation
The axis of rotation is through point A (0, 0) and is parallel to the diagonal BD. The diagonal BD runs from point B (l, 0) to point D (0, l).
Step 3: Calculate the Distances from the Axis
We need to find the perpendicular distances from each mass to the axis of rotation:
- For mass at A (0, 0): Distance = 0
- For mass at B (l, 0): Distance = l√2 (since the line BD has a slope of -1, the perpendicular distance can be calculated using geometry)
- For mass at C (l, l): Distance = l√2 (similar reasoning as for B)
- For mass at D (0, l): Distance = 0 (since it lies on the axis)
Step 4: Use the Parallel Axis Theorem
The moment of inertia I about the axis through A can be calculated using the formula:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass and d is the distance from the center of mass to the axis of rotation.
Step 5: Calculate Individual Moments of Inertia
The moment of inertia for each mass about the axis through A is:
- For mass at A: IA=m⋅02=0
- For mass at B: IB=m⋅(l√2)2=ml22
- For mass at C: IC=m⋅(l√2)2=ml22
- For mass at D: ID=m⋅02=0
Step 6: Sum the Moments of Inertia
Now, we sum the contributions from all four masses:
I=IA+IB+IC+ID=0+ml22+ml22+0=ml2
Step 7: Final Calculation
Since we have two masses contributing ml22 each, the total moment of inertia about the axis through A is:
I=ml2+ml2=2ml2
Step 8: Include the Contribution from the Parallel Axis Theorem
Since we are considering the axis through A and not the center of mass, we need to apply the parallel axis theorem for the total mass M=4m and the distance d=l√2:
I=2ml2+4m(l√2)2=2ml2+4m⋅l22=2ml2+2ml2=4ml2
Final Result
Thus, the moment of inertia of the system about the axis passing through A and parallel to BD is:
I=3ml2
We have four point masses, each of mass m, located at the corners of a square ABCD with side length l. The points are:
- A at (0, 0)
- B at (l, 0)
- C at (l, l)
- D at (0, l)
The axis of rotation is through point A (0, 0) and is parallel to the diagonal BD. The diagonal BD runs from point B (l, 0) to point D (0, l).
We need to find the perpendicular distances from each mass to the axis of rotation:
- For mass at A (0, 0): Distance = 0
- For mass at B (l, 0): Distance = l√2 (since the line BD has a slope of -1, the perpendicular distance can be calculated using geometry)
- For mass at C (l, l): Distance = l√2 (similar reasoning as for B)
- For mass at D (0, l): Distance = 0 (since it lies on the axis)
The moment of inertia I about the axis through A can be calculated using the formula:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass and d is the distance from the center of mass to the axis of rotation.
The moment of inertia for each mass about the axis through A is:
- For mass at A: IA=m⋅02=0
- For mass at B: IB=m⋅(l√2)2=ml22
- For mass at C: IC=m⋅(l√2)2=ml22
- For mass at D: ID=m⋅02=0
Now, we sum the contributions from all four masses:
I=IA+IB+IC+ID=0+ml22+ml22+0=ml2
Since we have two masses contributing ml22 each, the total moment of inertia about the axis through A is:
I=ml2+ml2=2ml2
Since we are considering the axis through A and not the center of mass, we need to apply the parallel axis theorem for the total mass M=4m and the distance d=l√2:
I=2ml2+4m(l√2)2=2ml2+4m⋅l22=2ml2+2ml2=4ml2
Thus, the moment of inertia of the system about the axis passing through A and parallel to BD is:
I=3ml2
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Video
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be:
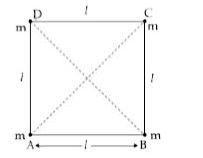
View SolutionFour point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
View Solution
Knowledge Check
Four point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
A√3ml2B3ml2Cml2D2ml2Four point masses, each of value m, are placed at the corners of square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is -
A2ml2B√3ml2C3ml2Dml2Four point masses each of value m, are placed at the corners of a square ABCD of side l, The moment of inertia of the system about an axis passing throught A and parallel to BD is
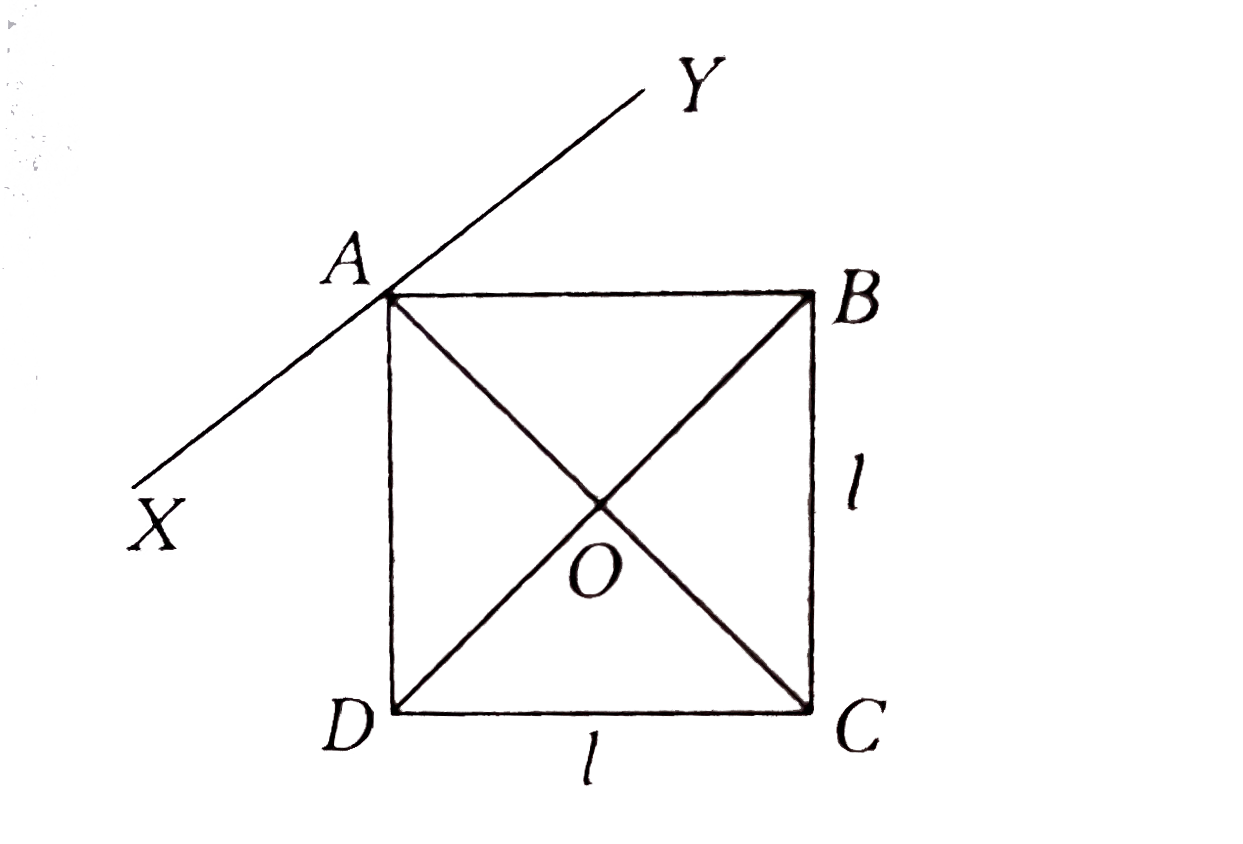 A√3ml2B3ml2Cml2D2ml2
A√3ml2B3ml2Cml2D2ml2
Four point masses, each of value m, are placed at the corners of a square ABCD of side 1. The moment of inertia of this system about an axis through A and parallel to BD is
View SolutionFour point masses, each of value m, are placed at the corners of a square ABCD, having each side of length L. What is the moment of inertia of this system about an axis passing through A and parallel to the diagonal BD?
View SolutionThree point masses each of mass m are placed at the corners of an equilateral triangle of side 'a'. Then the moment of inertia of this system about an axis passing along one side of the triangle is
View SolutionThree point masses each of mass m are placed at the corners of an equilateral triangle of side 'a' . Then the moment of inertia of this system about an axis passing along one side of the triangle is
View SolutionThree point masses each of mass m are placed at the corners of an equilateral triangle of side 'a'. Then the moment of inertia of this system about an axis passing along one side of the triangle is
View Solution