Four sources of sound each of sound level $10 d B$ are sounded together in phase , the resultant intensity level will be $({log}_{10} 2 = 0.3)$

A

$40 d B$

B

$26 d B$

C

$22 d B$

D

$13 d B$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Resulant ampulitude will become $4$ times.
Therefore , resultant intensity is $16$ times
$L_{2} - L_{1} = \frac{{log}_{10} (I_{2})}{I_{1}}$
or $I_{2} - 10 = 10 {log}_{10} (16)$
or $L_{2} = 22 d B$

|

Updated on:21/07/2023

Class 11 PHYSICS SOUND WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A sound has an intensity of $2 \times 10^{- 8} W / m^{2}$ . Its intensity level in decibels is $({log}_{10} 2 = 0.3)$
A $23$
B $3$
C $43$
D $4.3$
Question 2 - Select One
The intensity level of two sounds are 100 dB and 50 dB. What is the ratio of their intensities?
A $10^{1}$
B $10^{3}$
C $10^{5}$
D $10^{10}$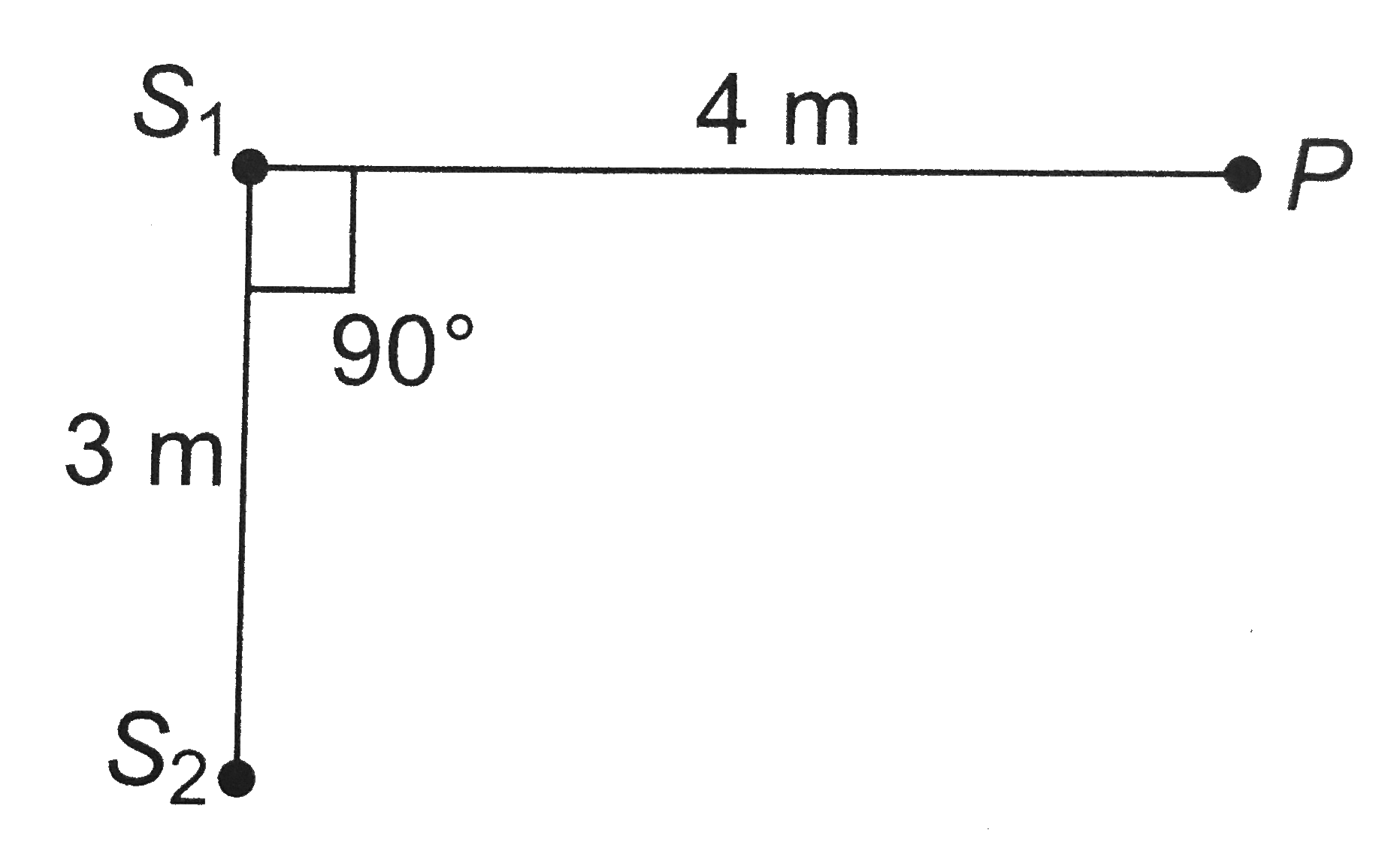
Question 3 - Select One

$S_{1}$ and $S_{2}$ are two coherent sources of sound of frequency $110 H z$ each they have no initial phase difference. The intensity at a point P due to $S_{1}$ is $I_{0}$ and due to $S_{2}$ is $4 I_{0}$ . If the velocity of sound is $330 m / s$ then the resultant intensity at P is
A $I_{0}$
B $9 I_{0}$
C $3 I_{0}$
D $8 I_{0}$

DC PANDEY-SOUND WAVES-Level 1 Objective

Home
Ask Doubt
Profile