From a single source, two wave trains are sent in two different string. The two wave equations are ((area of corss-section and tension of both string are same y1 = A sin (w1t−k1x)andy2=2Asin(w1t−k2z)Suppose u = energy density , P = power trasmitted and I = intensity of the wave, then match the following. 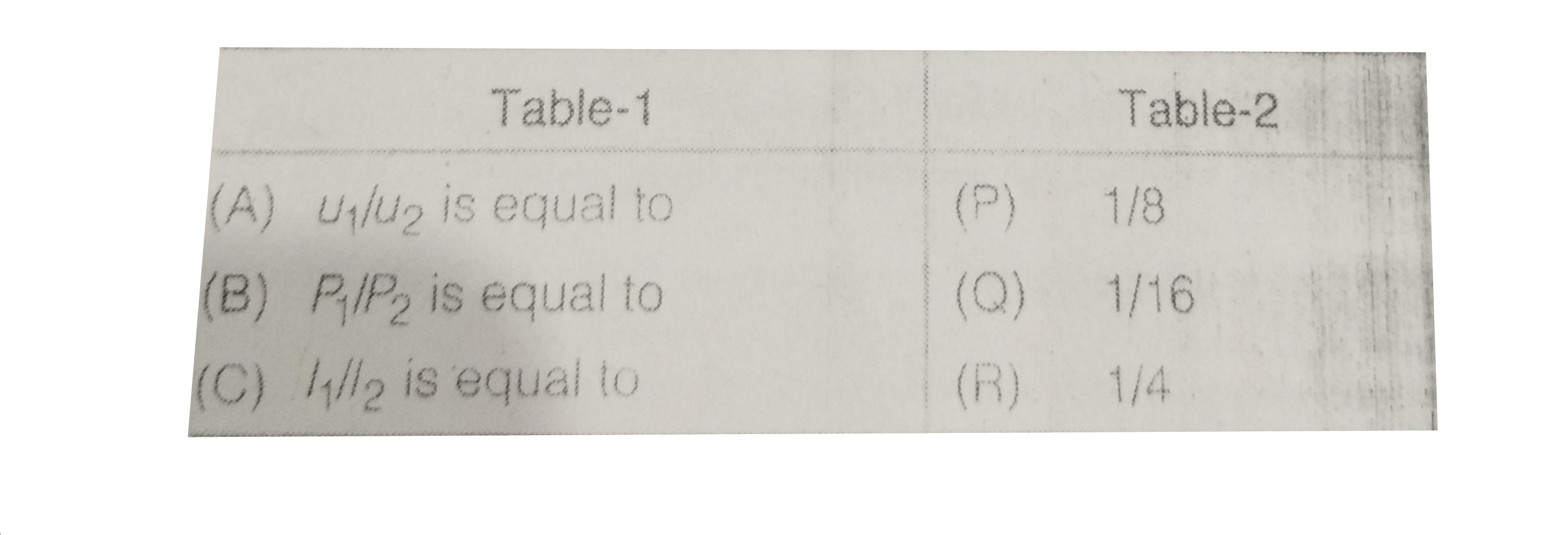
The correct Answer is:(a)Q, (b)P, (c )P
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions
19 Videos
- VECTORSBOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
Knowledge Check
Two waves y1=A1sin(ωt−β1),y2=A2sin(ωt−β2) Superimpose to form a resultant wave whose amplitude is
A√A21+A22+2A1A2cos(β1−β2)B√A21+A22+2A1A2sin(β1−β2)CA1+A2D|A1+A2|The resultant ampiltude of a vibrating particle by the superposition of the two waves y1=asin(ωt+π3)andy2=asinωt is :
AaB√2aC2aD√3aWave equations of two particles are given by y1=asin(ωt−kx),y2=asin(kx+ωt), then
AThey are moving in opposite directionBPhase between them is 90∘CPhase between them is 180∘DPhase between them is 0∘
A standing wave is formed by two harmonic waves, y1=Asin(kx−ωt)andy2=Asin(kx+ωt) travelling on a string in opposite directions. Mass density energy between two adjavent nodes on the string.
View SolutionEquations of two progressive wave are given by y1=asin(ωt+ϕ1) and y2=asin(ωt+ϕ2). IF amplitude and time period of resultant wave is same as that of both the waves, then (ϕ1−ϕ2) is
View SolutionLet the two waves y1=Asin(kx−ωt) and y2=Asin(kx+ωt) from a standing wave on a string . Now if an additional phase difference of ϕ is created between two waves , then
View SolutionThe stationary wave y = 2a sinkx cosωt in a stretched string is the result of superposition of y1=asin(kx−ωt) and
View SolutionThe stationary wave y = 2a sinkx cosωt in a stretched string is the result of superposition of y1=asin(kx−ωt) and
View Solution
