From a single source, two wave trains are sent in two different string. The two wave equations are ((area of cross-section and tension of both string are same y1 = A sin (w1t−k1x)andy2=2Asin(w1t−k2z)Suppose u = energy density , P = power trasmitted and I = intensity of the wave, then match the following. 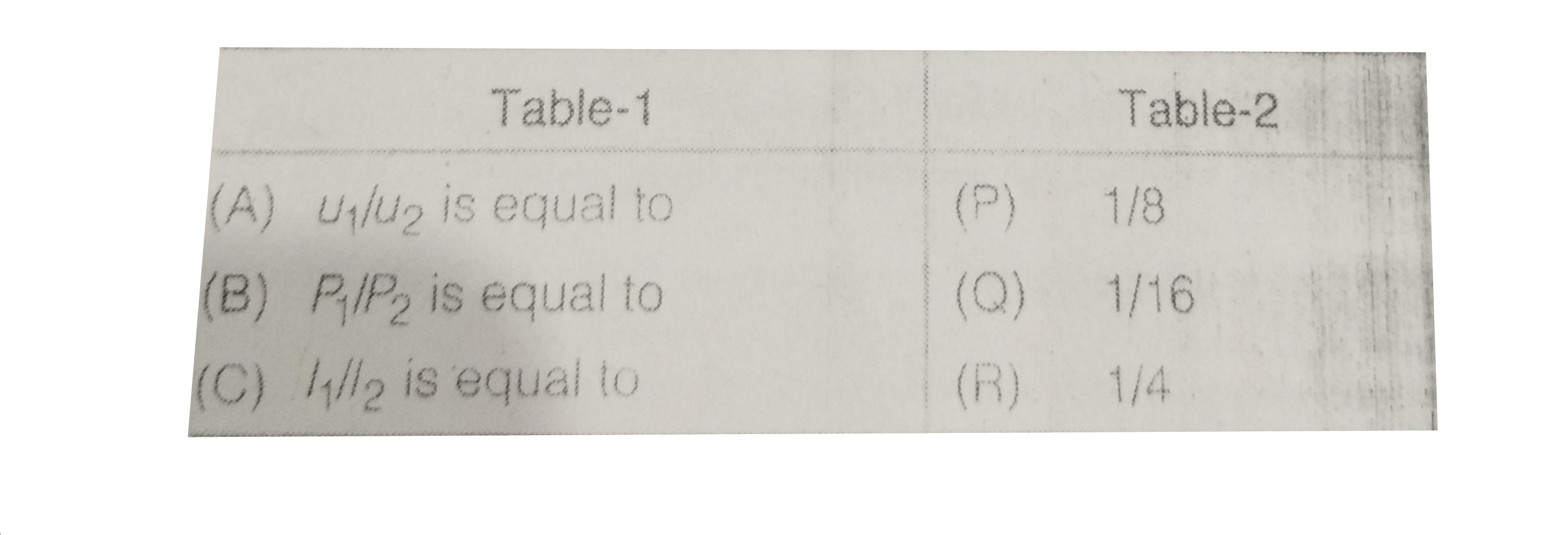
The correct Answer is:(a)Q, (b)P, (c )P
Step by step video & image solution for From a single source, two wave trains are sent in two different string. The two wave equations are ((area of cross-section and tension of both string are same y_(1) = A sin (w_(1)t-k_(1)x)and y_(2) = 2A sin (w_(1)t -k_(2)z)Suppose u = energy density , P = power trasmitted and I = intensity of the wave, then match the following. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions
20 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
Knowledge Check
Equations of two progressive wave are given by y1=asin(ωt+ϕ1) and y2=asin(ωt+ϕ2). IF amplitude and time period of resultant wave is same as that of both the waves, then (ϕ1−ϕ2) is
Aπ3B2π3Cπ6Dπ4Two waves are represented by the following equations
y1=5sin2π(10t−0.1x)
y2=10sin2π(20t−0.2x)
Ratio of intensites I2/I1 will beA1B2C4D16
When two progressive waves y1=4sin(2x−6t) and y2=3sin(2x−6t−π2) are superimposed, the amplitude of the resultant wave is
View SolutionTwo waves, whose equations are
y1=4sin(20t−x3)mandy2=3sin(20t−x3) m,
are superposed in a medium. Now,
View SolutionDetermine the resultant of two waves given by y1=4sin(200πt)andy2=3sin(200πt+π/2).
View SolutionTwo waves are passing through a region in the same direction at the same time . If the equation of these waves are
y1=asin(2π)λ(vt−x)
and y2=bsin(2π)λ[(vt−x)+x0]
then the amplitude of the resulting wave for x0=(λ/2) is
View SolutionBoth the strings, shown in figure, are made of same material and have same cross-section. The pulleys are light. The wave speed of transverse wave in the string AB is v1 and in CD it is v2, the v1/v2 is

View SolutionThe equation of a wave travelling on a string is given by Y(mn) = 8 sin[(5m−1x−(4s−1t]. Then
View Solution
