From the quantities given below , choose the one which is not indepndent of the choice of orientation of the coordinate axes:
(a) →P+→q
(b) ∣∣→P+→q−→r∣∣
(c) 2px+5qy
To solve the problem, we need to identify which of the given quantities is not independent of the choice of orientation of the coordinate axes.
1. Understanding Vector Addition and Subtraction:
- Vector addition and subtraction are operations that do not depend on the orientation of the coordinate axes. This means that if we add or subtract vectors, the result will remain the same regardless of how we choose to orient our axes.
2. Analyzing the First Option: →P+→q:
- This expression represents the addition of two vectors, →P and →q. Since vector addition is independent of the coordinate system, this quantity is independent of the choice of orientation of the coordinate axes.
3. Analyzing the Second Option: ∣∣→P+→q−→r∣∣:
- This expression involves the addition of →P and →q, followed by the subtraction of →r, and then taking the magnitude of the resultant vector. Similar to the first option, this operation is also independent of the coordinate axes because it involves vector addition and subtraction. Thus, this quantity is also independent of the choice of orientation of the coordinate axes.
4. Analyzing the Third Option: 2px+5qy:
- This expression is a scalar quantity that depends on the coordinates x and y. The values of x and y are determined by the orientation of the coordinate axes. If we change the orientation of the axes, the values of x and y will change, which will, in turn, affect the value of the entire expression 2px+5qy. Therefore, this quantity is dependent on the choice of orientation of the coordinate axes.
Conclusion:
The quantity that is not independent of the choice of orientation of the coordinate axes is:
(c) 2px+5qy
- Vector addition and subtraction are operations that do not depend on the orientation of the coordinate axes. This means that if we add or subtract vectors, the result will remain the same regardless of how we choose to orient our axes.
- This expression represents the addition of two vectors, →P and →q. Since vector addition is independent of the coordinate system, this quantity is independent of the choice of orientation of the coordinate axes.
- This expression involves the addition of →P and →q, followed by the subtraction of →r, and then taking the magnitude of the resultant vector. Similar to the first option, this operation is also independent of the coordinate axes because it involves vector addition and subtraction. Thus, this quantity is also independent of the choice of orientation of the coordinate axes.
- This expression is a scalar quantity that depends on the coordinates x and y. The values of x and y are determined by the orientation of the coordinate axes. If we change the orientation of the axes, the values of x and y will change, which will, in turn, affect the value of the entire expression 2px+5qy. Therefore, this quantity is dependent on the choice of orientation of the coordinate axes.
The quantity that is not independent of the choice of orientation of the coordinate axes is:
(c) 2px+5qy
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - TOUGH & TRICKY PROBLEMS
14 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) NCERT (Textbook Exercises)
25 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
Which of the following quantities are independent of the choice of orientation of the coordinate axes : →a+→, 3ax+2by, ∣∣→a+→b−→c∣∣, angle between →b and →c , λ→a , where λ is a scalar ?
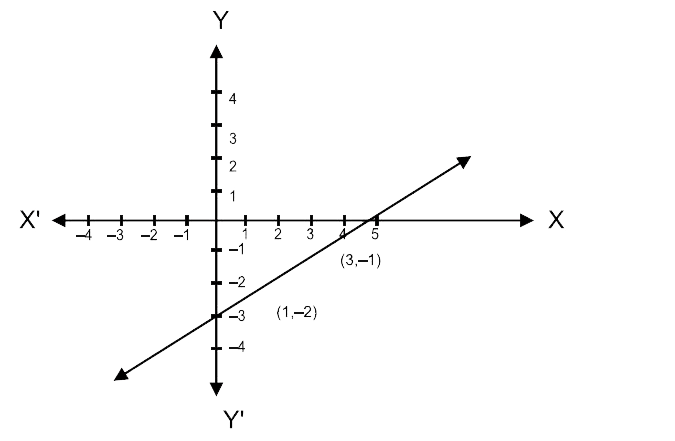
View SolutionFrom the choices given below choose the equation whose graph is given in
(i) x+2y=5
(ii) x-2y=5
(iii) y+2x=5
View Solution
Knowledge Check
A variable plane which remains at a constant distance P from the origin (0) cuts the coordinate axes in A, B and C
ALocus of centroid of tetrahedron OABC is x2y2+z2y2+z2x2=16p2(x2y2z2).BLocus of centroid of tetrahedron OABC is x2y2+z2y2+z2x2=4p2(x2y2z2).CParametric equation of the centroid of the the tetrahedron is of the form (p4sec(α)sec(β),p4sec(α)cosec(β),p4cosec(α))α,β∈(0,2π)−{π2,π,3π2}.DNone of theseGiven below is the diagram of a virus. In which one of the options A, B and C are correct ?
 AABCRNACapsidTobacco Mosaic VirusBABCDNACapsidTobacco Mosaic VirusCABCRNALipidTobacco Mosaic VirusDABCRNAProteinHIV
AABCRNACapsidTobacco Mosaic VirusBABCDNACapsidTobacco Mosaic VirusCABCRNALipidTobacco Mosaic VirusDABCRNAProteinHIVTwo vectors →Pand→Q lie one plane. Vectors →R lies in a differenct plane. In such a case, →P+→Q+→R
Acan be zeroBcannot be zeroClies in the sama plane as →P or →QDlies in the plane different from that of any two of 3 vectors
Suppose that →p,→qand→r are three non-coplanar vectors in R3. Let the components of a vectors →s along →p,→qand→r be 4, 3 and 5, respectively. If the components of this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x,yandz, respectively, then the value of 2x+y+z is
View SolutionA cube in the first octant has sides OP, OQ and OR of length 1, along the z-axis, y-axis and z-axis, respectively, where O(0, 0, 0) is the origin. Let the centre of the cube be at S(12.12,12) and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If →p=−→SP,→q=−−→SQ,→r=−−→SR and →t=−→ST, then the value of ∣∣(→p×→q)×(→r×→t)∣∣ is:
View SolutionSuppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is
View SolutionLet →p,→q,→r,→s are non - zero vectors in which no two of them are perpenedicular and no three of them are coplanar. If (→p×→r).(→p×→s)+(→r×→p).(→q×→s)=k[(→p×→q).(→s×→r)], then the value of k2 is equal to
View SolutionIf →P×→Q=→R, then which of the following statements is not true ?
View Solution
