From the top of a hill 480 m high , a projectile is fired horizontally with a speed of 96m/s . Calculate
(i) the time taken by projectile to reach the ground .
(ii) the distance of the target from the hill .
(iii) the velocity with which the projectile hits the ground . Take g=10ms−2
To solve the problem step by step, we will break it down into three parts as per the question.
Given:
- Height of the hill, h=480m
- Horizontal speed of the projectile, u=96m/s
- Acceleration due to gravity, g=10m/s2
(i) Time taken by the projectile to reach the ground
1. Identify the motion: The projectile is fired horizontally, so its initial vertical velocity uy=0.
2. Use the second equation of motion: The vertical motion can be described by the equation:
h=uyt+12gt2
Since uy=0, the equation simplifies to:
h=12gt2
3. Substitute the values:
480=12⋅10⋅t2
480=5t2
4. Solve for t2:
t2=4805=96
5. Take the square root:
t=√96=4√6s
(ii) Distance of the target from the hill
1. Calculate horizontal distance: The horizontal distance d traveled by the projectile can be calculated using:
d=u⋅t
2. Substitute the values:
d=96⋅4√6
3. Calculate d:
d=384√6m
(iii) Velocity with which the projectile hits the ground
1. Calculate vertical velocity at impact: The vertical velocity vy just before hitting the ground can be calculated using:
vy=uy+gt
Since uy=0:
vy=0+10⋅4√6
vy=40√6m/s
2. Calculate the resultant velocity: The resultant velocity v can be found using the Pythagorean theorem:
v=√u2+v2y
v=√(96)2+(40√6)2
v=√9216+9600=√18816
v≈137.1m/s
Summary of Results:
- (i) Time taken to reach the ground: t=4√6s
- (ii) Distance of the target from the hill: d=384√6m
- (iii) Velocity with which the projectile hits the ground: v≈137.1m/s
- Height of the hill, h=480m
- Horizontal speed of the projectile, u=96m/s
- Acceleration due to gravity, g=10m/s2
2. Use the second equation of motion: The vertical motion can be described by the equation:
h=uyt+12gt2
Since uy=0, the equation simplifies to:
h=12gt2
3. Substitute the values:
480=12⋅10⋅t2
480=5t2
4. Solve for t2:
t2=4805=96
5. Take the square root:
t=√96=4√6s
d=u⋅t
2. Substitute the values:
d=96⋅4√6
3. Calculate d:
d=384√6m
vy=uy+gt
Since uy=0:
vy=0+10⋅4√6
vy=40√6m/s
2. Calculate the resultant velocity: The resultant velocity v can be found using the Pythagorean theorem:
v=√u2+v2y
v=√(96)2+(40√6)2
v=√9216+9600=√18816
v≈137.1m/s
- (i) Time taken to reach the ground: t=4√6s
- (ii) Distance of the target from the hill: d=384√6m
- (iii) Velocity with which the projectile hits the ground: v≈137.1m/s
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (A. Multiple Choice Questions)
30 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (B. Multiple Choice Questions)
38 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Revision Exercises (Long Answer Question)
6 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
A projectile is fired horizontally with a velocity of 98ms−1 from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.
View SolutionA particle is fired horizontally with a velocity of 100ms−1 for the top of a hill 400m high. Find (i) the time taken to reach the ground (ii) thedistance of the target from the hill and (iii) the velocity with which the projectile hits the ground. Take g=10ms−2.
View Solution
Knowledge Check
A projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. (g=9.8m/s2)
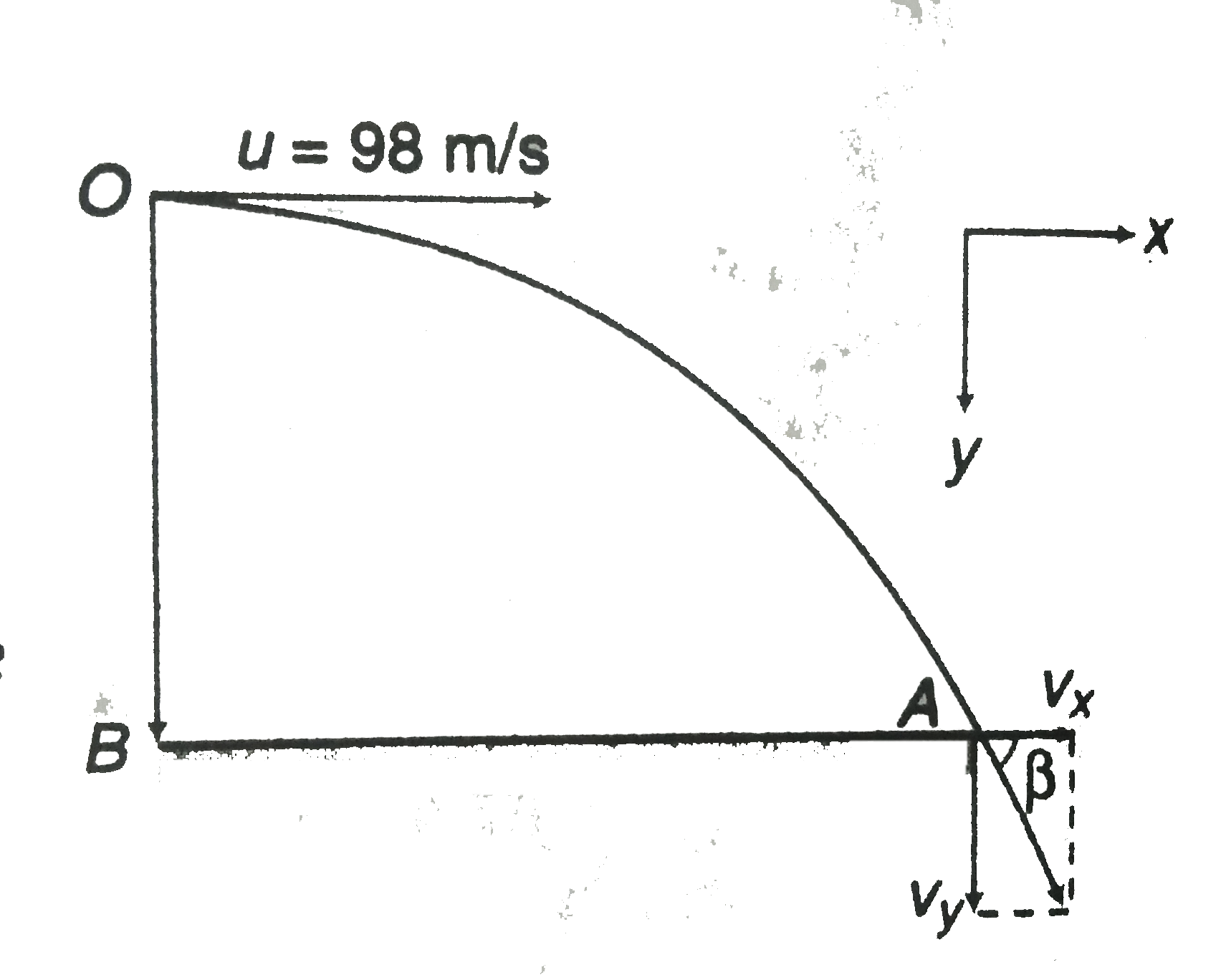 .A12s , 980m , 98(√2)m/s β=45B10s , 98m , 98(√2)m/s β=45C10s , 980m , 98m/s β=45D10s , 980m , 98(√2)m/s β=45
.A12s , 980m , 98(√2)m/s β=45B10s , 98m , 98(√2)m/s β=45C10s , 980m , 98m/s β=45D10s , 980m , 98(√2)m/s β=45A projectile is fired horizontally from a tower which is 25 ft high from the level of the ground and reaches the ground at a horizontal distance of 1000 ft. The initial velocity is
A200ft/secB400ft/secC600ft/secD800ft/secA bullet is fired vertically up from a 400 m tall tower with a speed 80 m/s. If g is taken as 10m/s2, the time taken by the bullet to reach the ground will be
A8 sB16 sC20 sD24 s
A stone is thrown up with a velocity of 18ms−1 from a 25 m high deck, Calculate the total time taken by stone to reach the ground .
View SolutionA particle is dropped from a tower 180 m high. How long does it take to reach the ground ? What is the velocity when it touches the ground ? Take g=10m/s2.
View SolutionAn iron ball of mass 3 kg is released from a height of 125 m and falls freely to the ground. Assuming that the value of g is 10m/s2, calculate
(i) time taken by the ball to reach the ground
(ii) velocity of the ball on reaching the ground
(iii) the height of the ball at half the time if takes to reach the ground.
View SolutionA plane is flying horizontal at a height of 1000m with a velocity of 100ms−1 when a bomb is released from it. Find (i) the time taken by it to reach the ground (ii) the velocity with which the bomb hits the target and (iii) the distance of the target.
View SolutionFrom the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is
View Solution
